
Introducción a la función recursiva en Java
Una función recursiva es la que se llama a sí misma una o muchas veces. Una función recursiva se utiliza en situaciones en las que el mismo conjunto de operaciones debe realizarse una y otra vez hasta que se alcance el resultado. Realiza varias iteraciones y la declaración del problema se vuelve más simple con cada iteración.
Siempre se debe especificar un límite base al escribir una función recursiva; de lo contrario, se produce un error de desbordamiento de pila. Una pila es un área de memoria reservada para mantener las invocaciones de métodos. El error se debe a que la función comienza a ejecutarse continuamente, ya que no podrá encontrar la condición limitante y, por lo tanto, finalmente agotará la memoria asignada. Entonces, para evitar el desbordamiento de la pila, definimos ciertas condiciones básicas con la ayuda de declaraciones "if … else" (o cualquier otra declaración condicional) que haga que la función de recursión se detenga tan pronto como se complete el cálculo requerido.
Tipos de recursión en Java
Hay 2 tipos de recursividad en Java. Son:
1. Recursión directa
Sintaxis:
Aquí la función1 se llama a sí misma continuamente, por lo tanto, es una función recursiva.
public static void main(String() args)(
//few lines of code
function();
//few lines of code
)
function() (
//few lines of code
function();
//few lines of code
)
Ejemplo
El factorial de un número es un ejemplo de recursión directa. El principio básico de la recursividad es resolver un problema complejo dividiéndolo en otros más pequeños. Por ejemplo, en el caso del factorial de un número, calculamos el factorial de "i" si conocemos su factorial de "i-1".
Código:
public class Factorial (
static int fact(int i)(
if (i == 1)
return 1;
else
return(i * fact(i-1));
)
public static void main(String() args) (
System.out.println("The factorial of given number 6 is: "+fact(6));
)
)
Salida:

2. Recursión indirecta / mutua
Una función1 que llama a otra función2, que a su vez llama a la función1 directa o indirectamente, se llama función recursiva indirecta.
Sintaxis:
Considere 2 funciones llamadas function1 () y function2 (). Aquí function1 llama a function2 y function2 llama a function1.
function1()(
//few lines of code
function2();
//few lines of code
)
function2()(
//few lines of code
function1();
//few lines of code
)
Ejemplo
Para mostrar la recursividad indirecta, tomamos el siguiente programa utilizado para averiguar si un número dado es par o impar de la entrada dada.
Código:
import java.util.Scanner;
public class IndirectRecursion (
public static boolean oddNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return false;
) else (
return evenNum(i-1);
)
)
public static boolean evenNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return true;
) else (
return oddNum(i-1);
)
)
public static void main(String() args) (
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
)
)
Salida:
Ejemplos de recursión en Java
Aquí hay algunos ejemplos más para resolver los problemas utilizando el método de recursión.
Ejemplo # 1 - Secuencia de Fibonacci
Se dice que un conjunto de números "n" está en una secuencia de Fibonacci si número3 = número1 + número2, es decir, cada número es una suma de sus dos números anteriores. Por lo tanto, la secuencia siempre comienza con los dos primeros dígitos, como 0 y 1. El tercer dígito es una suma de 0 y 1 que da como resultado 1, el cuarto número es la suma de 1 y 1 que da como resultado 2, y la secuencia continúa.
Consulte el siguiente código en Java para generar una secuencia de Fibonacci:
public class FibonacciSeries(
static int num1=0, num2=1, num3=0;
static void fibonacci(int n)(
if(n>0)(
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
)
)
public static void main(String args())(
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
)
)
Salida:

Aquí los dos primeros números se inicializan a 0 y 1 y se imprimen. Las variables "num1", "num2" y "num3" se utilizan para generar la secuencia requerida. La variable "num3" se obtiene agregando "num1" y "num2" y los números se desplazan una posición a la izquierda al barajar como se muestra en el código. La función "Fibonacci" se llama recursivamente aquí y en cada iteración, el valor de "n" se reduce en 1. Por lo tanto, la recursión sale tan pronto como "n" alcanza el valor 0.
Ejemplo # 2 - Torre de Hanoi
Este es un problema matemático clásico que tiene 3 polos y un número "n" de discos con diferentes tamaños. El rompecabezas es el siguiente:
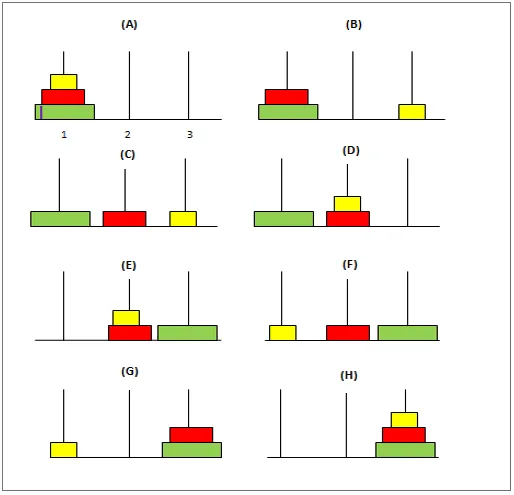
Al principio, el primer poste tendrá los discos dispuestos de manera que el disco más grande de todos esté en la parte inferior y el más pequeño en la parte superior del poste. El objetivo es mover estos discos del primer polo al tercer polo manteniendo los discos en la misma posición que en el primero. Las siguientes son algunas condiciones a tener en cuenta al cambiar estos discos:
1. A la vez, solo se debe mover un disco.
2. En el proceso, no está permitido colocar un disco más grande sobre uno más pequeño.
3. El segundo polo (medio) se puede utilizar para mediar mientras se transfieren los discos del primero al segundo polo.
El siguiente es el código Java que se puede usar para resolver el rompecabezas:
Código:
public class TowerOfHanoi (
public static void main(String() args) (
int count = 3;
tower(count, 'A', 'B', 'C');
)
public static void tower(int first, char disk1, char temp, char disk2) (
if (first == 1) (
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
) else (
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
)
)
)
Salida:
Aquí la variable "cuenta" representa el número de discos que se utilizarán. La función "torre" es la función recursiva utilizada para mover los discos de la barra 1 a la barra 3. Se puede proporcionar una solución simple a este problema al considerar 2 discos al principio.
- Primero, comenzamos moviendo el disco 1 de la barra 1 a la barra 2.
- A continuación, movemos el disco2 a la barra 3.
- Finalmente, terminamos moviendo el disco 1 a la barra 3 completando la solución requerida.
Este mismo principio se aplica para el número "n" de discos moviendo (n-1) el disco de la barra 1 a 2 y siguiendo pasos similares a los anteriores.
Ventajas de la recursividad en Java
- El código es fácil de escribir y mantener.
- El mejor método para encontrar los resultados donde se requiere una gran cantidad de iteraciones.
Desventajas de la recursividad en Java
- Las funciones recursivas usan más memoria. Esto se debe a que cada vez que se llama a una función recursiva; la asignación de memoria se realiza nuevamente para las variables en la pila. Y la asignación de memoria respectiva se libera tan pronto como se devuelven los valores variables.
- Este proceso de asignación de memoria lleva más tiempo, por lo tanto, la ejecución suele ser lenta.
Conclusión
Las funciones recursivas son relativamente más simples de codificar, pero tampoco son tan eficientes en comparación con los otros métodos existentes. Por lo tanto, se utilizan principalmente en casos donde el tiempo dado para el desarrollo es menor y también donde se puede observar un patrón significativo en el problema.
Artículos recomendados
Esta es una guía de Recursión en Java. Aquí discutimos los tipos de recursión en Java junto con sus diferentes ejemplos con las ventajas y desventajas. También puede consultar los siguientes artículos para obtener más información.
- JScrollPane en Java
- Funciones matemáticas en Java
- Funciones matemáticas en Java
- Constructor en Java
- Función recursiva en Python
- Programa Factorial en JavaScript