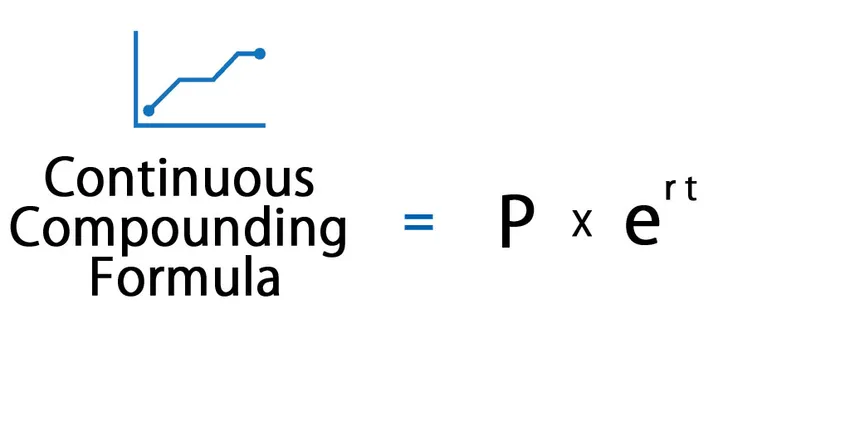
Fórmula de composición continua

Fórmula de composición continua (Tabla de contenido)

Fórmula de composición continua
Calculadora de capitalización continua
Fórmula de composición continua en Excel (con plantilla de Excel)

Antes de saltar al concepto de capitalización continua, primero comprendamos qué es el interés compuesto. El interés compuesto significa que el interés que los inversionistas ganan cada año se agrega a su capital principal, de modo que la cantidad no solo crece, sino que crece a una tasa creciente que la tasa de interés simple, es uno de los conceptos más útiles en las finanzas. Es la base de todo, desde un plan de inversión a largo plazo en el mercado de acciones hasta el plan de ahorro personal. También se ocupa de los efectos de la inflación en el monto y la importancia de pagar la deuda. Calculadora (plantilla de Excel).

Para la capitalización continua se agrega una tasa de interés en cada momento. Esto hace que el cálculo sea difícil. Ninguna institución financiera lo utiliza para cobrar tasas de interés, ya que hay poca diferencia en el monto compuesto continuo y el monto compuesto diario. Los bancos utilizan el monto de interés compuesto diario en algunos de sus productos.

La fórmula para la capitalización continua es la siguiente:

La fórmula de capitalización continua calcula el interés ganado que se capitaliza continuamente durante un período de tiempo infinito.

dónde,

P = Importe principal (valor actual del importe)

t = Tiempo (el tiempo es años)

r = Tasa de interés.

El cálculo anterior supone un interés compuesto constante durante un período de tiempo infinito. Como el período de tiempo mencionado es infinito, la función de exponente (e) ayuda a multiplicar el monto de la inversión actual. Esto se multiplica por la tasa de interés actual y el período de tiempo. A pesar del gran número de inversiones, la diferencia entre el interés total ganado a través de la capitalización continua en excel es la misma en comparación con la capitalización de intereses tradicional.

Ejemplos y explicación de la fórmula de composición continua

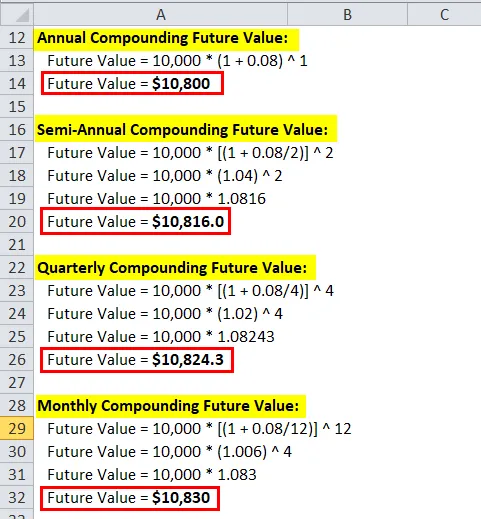
Calcule el interés compuesto sobre el capital $ 10, 000 con una tasa de interés del 8% y un período de tiempo de 1 año. La frecuencia de capitalización es una capitalización anual, semestral, trimestral, mensual y continua.

Puede descargar esta plantilla de composición continua aquí - Plantilla de composición continua

Valor futuro compuesto anual:

Valor futuro = 10, 000 * (1 + 0.08) 1
Valor futuro = $ 10, 800

Valor futuro compuesto semestral:

Valor futuro = 10, 000 * ((1 + 0.08 / 2)) 2
Valor futuro = 10, 000 * (1.04) 2
Valor futuro = 10, 000 * 1.0816
Valor futuro = $ 10, 816.0

Valor futuro compuesto trimestral:

Valor futuro = 10, 000 * ((1 + 0.08 / 4)) 4
Valor futuro = 10, 000 * (1.02) 4
Valor futuro = 10, 000 * 1.08243
Valor futuro = $ 10, 824.3

Valor futuro compuesto mensual:

Valor futuro = 10, 000 * ((1 + 0.08 / 12)) 12
Valor futuro = 10, 000 * (1.006) 4
Valor futuro = 10, 000 * 1.083
Valor futuro = $ 10, 830

Valor Futuro Compuesto Continuo:

Valor futuro = 10, 000 * e ^0.08
Valor futuro = 10, 000 * 1.08328
Valor futuro = $ 10, 832.87

Como se puede ver en el ejemplo anterior de cálculos de capitalización con diferentes frecuencias, el interés calculado a partir de capitalización continua es $ 832.9, que es solo $ 2.9 más que la capitalización mensual. Por lo tanto, se trata de utilizar una tasa de interés compuesta mensual o diaria en la vida práctica que la tasa de interés compuesta continua.

Significado y uso de la fórmula de composición continua

La importancia de la fórmula de composición continua es:

En lugar de una capitalización continua de intereses sobre una base anual, trimestral o mensual, la capitalización continua sobresaliente reinvertirá de manera eficiente las ganancias perpetuamente.
El efecto de capitalización continua permite que la capitalización continua del monto de interés se reinvierta a la misma tasa de interés, lo que le da la oportunidad a un inversor de obtener rendimientos a una tasa exponencial.
La capitalización continua determina que no solo la cantidad del principal generará dinero, sino que también la capitalización continua de la cantidad de interés también seguirá multiplicando la cantidad.

La capitalización se puede realizar de forma anual, semestral, trimestral, diaria o continua. La diferencia entre estos períodos de tiempo es que, después de terminar el período de tiempo, cualquier interés que se gane se trata como nuevo principal. Por ejemplo, si la frecuencia de capitalización es semestral, el interés se agregará al capital después de seis meses, este ciclo continúa hasta el vencimiento. Igual es el caso con otro marco de tiempo, para el interés anual se agrega después de un año, para el trimestre se agrega el interés después de tres meses, para el interés diario se agrega al día siguiente.

Calculadora de capitalización continua

Puede usar la siguiente calculadora de capitalización continua

PAG
r
t
Fórmula de composición continua =

Fórmula de composición continua =	P xe ^(rxt)
=	0 xe ^{(0 x 0)} = 0

Fórmula de composición continua en Excel (con plantilla de Excel)

Aquí haremos el mismo ejemplo de la fórmula de composición continua en Excel. Es muy fácil y simple. Debe proporcionar las tres entradas, es decir, el monto principal, la tasa de interés y el tiempo.

Puede calcular fácilmente la composición continua utilizando la fórmula en la plantilla proporcionada.

Primero, necesitamos calcular la cantidad de capitalización continua usando la fórmula

entonces, necesitamos calcular los efectos del mismo en la composición regular:

Artículos recomendados

Esta ha sido una guía para una fórmula de composición continua. Aquí discutimos sus usos junto con ejemplos prácticos. También le proporcionamos una Calculadora de capitalización continua con una plantilla de Excel descargable. También puede consultar los siguientes artículos para obtener más información: