
Fórmula de variación de cartera (tabla de contenido)
- Fórmula de variación de cartera
- Ejemplos de fórmula de variación de cartera (con plantilla de Excel)
Fórmula de variación de cartera
La variación de la cartera es una medida de dispersión de los rendimientos de una cartera. Se refiere a los rendimientos totales de la cartera durante un período de tiempo particular. La fórmula de variación de cartera se usa ampliamente en la teoría moderna de cartera. La fórmula de variación de la cartera se mide al cuadrar los pesos de las acciones individuales en la cartera y luego multiplicarla por la desviación estándar de los activos individuales en la cartera y también cuadrarla. Los números se suman luego por la covarianza de los activos individuales multiplicada por dos, también multiplicada por los pesos de cada acción, y también multiplicada por una correlación entre las diferentes acciones presentes en la cartera. Por lo tanto, la fórmula se puede resumir como
Variance = (w(1)^2 * o(1)^2) + (w(2)^2 * o(2)^2) + (2 * (w(1)*o(1)*w(2)*o(2)*q(1, 2)))
Dónde están los símbolos: -
- W (1) : Peso de una acción en la cartera al cuadrado.
- O (1): la desviación estándar de un activo en la cartera al cuadrado.
- W (2): Peso del segundo stock en la cartera al cuadrado.
- O (2): la desviación estándar del segundo activo en la cartera al cuadrado.
- Q (1, 2): la correlación entre los dos activos en la cartera se ha denotado como q (1, 2).
Ejemplos de fórmula de variación de cartera (con plantilla de Excel)
Tomemos un ejemplo para comprender el cálculo de la fórmula de variación de cartera de una mejor manera.
Puede descargar esta plantilla de Excel de fórmula de variación de cartera aquí - Plantilla de Excel de fórmula de variación de carteraFórmula de variación de cartera - Ejemplo # 1
Suponga que el stock A, el stock B, el stock C son acciones inmobiliarias en una cartera que tienen pesos en la cartera del 20%, 35% y 45% respectivamente. La desviación estándar de los activos es 2.3%, 3.5% y 4%. El coeficiente de correlación entre A y B es 0.6 entre A y C es 0.8 y Entre B y C es 0.5.
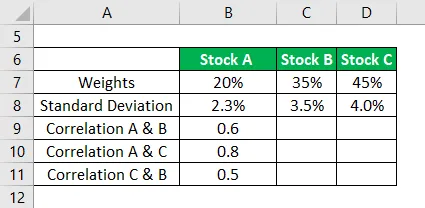
La variación de la cartera se calcula utilizando la fórmula que se proporciona a continuación
Varianza = (w (1) 2 * o (1) 2) + (w (2) 2 * o (2) 2) + (w (3) 2 * o (3) 2) + (2 * (w (1) o (1) w (2) o (2) q (1, 2)) + (2 * (w (1) o (1) w (3) o (3) q ( 1, 3)) + (2 * (w (2) o (2) w (3) o (3) q (2, 3)))
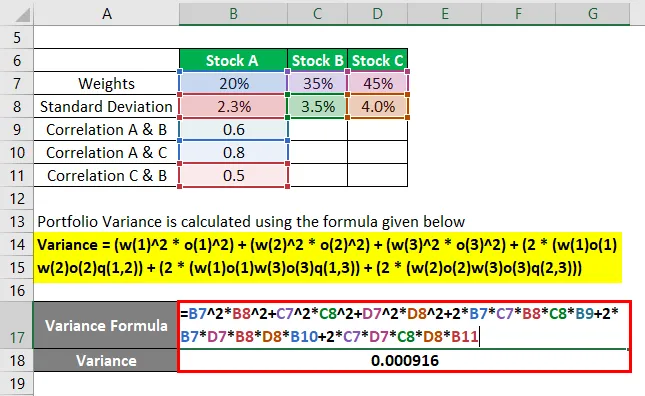
La variación de la cartera se convertirá
- Varianza = (20% 2 * 2.3% 2) + (35% 2 * 3.5% 2) + (45% 2 * 4% 2) + (2 * (20% * 35% * 2.3% * 3.5 * 0.6)) + (2 * (20% * 45% * 2.3% * 4% * 0.8)) + (2 * (35% * 45% * 3.5% * 4% * 0.5))
- Varianza = 0.000916
Fórmula de variación de cartera - Ejemplo # 2
Las acciones A y B son dos acciones inmobiliarias en una cartera con un rendimiento del 6% y 11% y el peso de las acciones A es del 54% y el peso de las acciones B es del 46%. La desviación estándar de A y B es 0.1 y 0.25. Además, tenemos información de que la correlación entre las dos acciones es 0.1
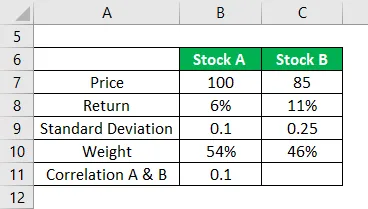
La variación de la cartera se calcula utilizando la fórmula que se proporciona a continuación
Variance = (w(1)^2 * o(1)^2) + (w(2)^2 * o(2)^2) + (2 * (w(1)*o(1)*w(2)*o(2)*q(1, 2)))
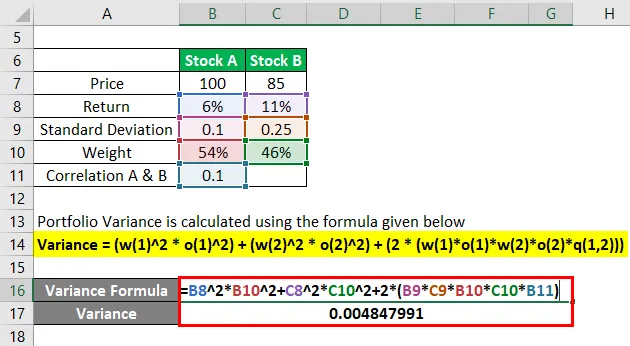
La variación de la cartera se convertirá
- Varianza = (6% 2 * 54% 2) + (11% 2 * 46% 2) + (2 * (0.1 * 0.25 * 54% * 46 * 0.1))
- Varianza = 0.004847991
Explicación
La fórmula de variación de cartera se calcula mediante los siguientes pasos:
Paso 1: Primero, el peso de las acciones individuales presentes en la cartera se calcula dividiendo el valor de esa acción en particular por el valor total de la cartera.
Paso 2: Los pesos después de ser calculados se cuadran.
Paso 3: La desviación estándar de la acción de la media se calcula calculando primero la media de la cartera y luego restando el rendimiento de esa acción individual de la rentabilidad media de la cartera.
Paso 4: Las desviaciones estándar de las existencias individuales se calculan y cuadran.
Paso 5: Luego se multiplica por sus respectivos pesos en la cartera.
Paso 6: La correlación de las existencias presentes en la cartera se calcula multiplicando la covarianza entre las existencias de la cartera con la desviación estándar del número de existencias de la cartera.
Paso 7: la fórmula se multiplica por 2.
Relevancia y usos de la variación de la cartera
- La fórmula de variación de la cartera ayuda al analista a comprender la variación de la cartera y, en caso de que el analista haya comparado el rendimiento de su cartera cuando un determinado índice o cualquier otro fondo que opere en el mercado, también puede verificar la variación de la misma.
- También es útil para encontrar la correlación entre los dos activos. La variación le dice al analista cuán estrechamente relacionadas están las acciones presentes en la cartera.
- La variación de la cartera también es una medida de riesgo, una cartera cuando muestra más variación de la media significa que la cartera es una cartera mucho más riesgosa y necesita un análisis detallado. La variación de una cartera se puede reducir eligiendo valores que estén correlacionados negativamente, por ejemplo. acciones y bonos.
Artículos recomendados
Esta ha sido una guía para la fórmula de variación de cartera. Aquí discutimos Cómo calcular la varianza de la cartera junto con ejemplos prácticos. También proporcionamos una plantilla de Excel descargable. También puede consultar los siguientes artículos para obtener más información:
- ¿Cómo calcular el rendimiento esperado?
- Fórmula para el margen de contribución
- Fórmula de elasticidad de precios
- Calculadora para la fórmula del margen de contribución
- Estado de ingresos del margen de contribución
- Fórmula de elasticidad | Ejemplo con plantilla de Excel