
Introducción a la serie de Fibonacci
La serie de Fibonacci radica en el proceso de que cada número actúa como una suma de dos valores anteriores y la secuencia siempre comienza con los enteros base 0 y 1. Los números de Fibonacci están relacionados muscularmente con la proporción áurea. En este tema, vamos a aprender sobre la serie Fibonacci en Java.
Fórmula: an = an - 2 + an - 1
| Serie de Fibonacci para los primeros 21 números | ||||||||||||||||||||
| F 0 | F 1 | F 2 | F 3 | F 4 | F 5 | F 6 | F 7 | F 8 | F 9 | F 10 | F 11 | F 12 | F 13 | F 14 | F 15 | F 16 | F 17 | F 18 | F 19 | F 20 |
| 0 0 | 1 | 1 | 2 | 3 | 5 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 | 6765 |
Aplicaciones clave
Aquí están las aplicaciones clave de la serie Fibonacci en Java a continuación.
- Conversión de millas a kilómetros y kilómetros a millas.
- Algunas instancias de metodología ágil
- El cálculo del análisis del tiempo de ejecución del algoritmo de Euclides se lleva a cabo utilizando esta técnica en serie.
- Algunos generadores de números pseudoaleatorios usan matemáticamente las estadísticas de Fibonacci.
- El proceso de planificación del póker implica el uso de esta técnica.
- La técnica de estructura de datos del montón de Fibonacci se logra utilizando la técnica de la serie Fibonacci.
- En óptica, mientras que un rayo de luz brilla en un punto de vista desde el principio hasta el final de dos placas translúcidas apiladas de materiales diferentes de índices de refracción diferentes, puede devolver tres superficies: el pináculo, el centro y las superficies de base de las dos placas. . El número de trayectoria de rayo diferente para tener kreflexiones, para k> 1, es el (\ display style k), el número de Fibonacci.
Programa de la serie Fibonacci (programa no recursivo)
// Fibonacci series program
public class Fibonacci (
// main program
public static void main(String() args) (
int count = 10, var1 = 0, var2 = 1;
System.out.print("First " + count + " terms: ");
// Fibonacci series formation loop
for (int i = 1; i <= count; ++i)
(
System.out.print(var1 + " + ");
int added_sum= var1 + var2;
var1 = var2;
var2 = added_sum;
)
)
)
Salida:
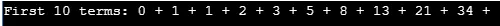
Explicación: Este programa calcula la serie de Fibonacci para un rango dado de números. aquí este proceso se logra sin utilizar una técnica recursiva. El algoritmo del programa se redacta línea por línea a continuación,
Algoritmo de programa
- Se declara una clase raíz Fibonacci con la necesidad de que todos los códigos de programa integrados en esta clase aborden la funcionalidad de lograr una serie de números Fibonacci.
- Dentro de la clase raíz, se declara el método principal. El método principal actúa, como regla, un método Java significativo. la ejecución de JVM no tendrá lugar sin la presencia del método principal en el programa. La explicación de varios subcomponentes del método principal se expresa a continuación.
- A continuación, la sección de inicialización variable está implícita. Esta sección implica la inicialización de tres variables diferentes. Dos de ellos son para lograr la lógica de Fibonacci a través de un intercambio de valores de nivel variable y otra variable se aplica para regular el recuento de valores para los que se necesita generar la lógica de Fibonacci.
- La lógica clave para el programa de la serie Fibonacci se logra usando el siguiente bucle dado en la sección del programa.
for (int i = 1; i <= count; ++i)
(
System.out.print(var1 + " + ");
int added_sum= var1 + var2;
var1 = var2;
var2 = added_sum;
)
- La lógica detrás de esto para la sección de bucle es la siguiente: inicialmente, se realiza un rango de valores en un bucle, el bucle ocurre con un incremento en el valor del rango para cada flujo que tiene lugar. Además, en cada flujo, el valor de las dos variables de intercambio se resume en una tercera variable.
- Después de resumir, el segundo valor de la variable está implícito en la primera variable, por lo que esto hace que el primer valor de la variable se elimine de este proceso. En el siguiente paso, el valor sumado se asigna a la segunda variable.
Entonces, al final de esta instancia para un solo flujo lógico, se aplican los siguientes eventos,
1. El valor de la primera variable se elimina.
2. El valor de la segunda variable existente se rellena en la primera variable.
3. El valor sumado se traslada a la segunda variable.
En el proceso de realizar la siguiente secuencia lógica para el recuento de valores dado que se necesita, se puede lograr la serie de Fibonacci.
Programa de la serie Fibonacci (uso de matrices)
import java.util.Arrays;
public class Main (
public static void main(String() args) (
int Count = 15;
long() array = new long(Count);
array(0) = 0;
array(1) = 1;
for (int x = 2; x < Count; x++) (
array(x) = array(x - 1) + array(x - 2);
)
System.out.print(Arrays.toString(array));
)
)
Salida:

Explicación: implica la lógica del programa redactada anteriormente, pero en este caso, las entradas de Fibonacci se almacenan como parte de las matrices. Entonces, todas las operaciones mencionadas anteriormente se llevan a cabo con respecto a una matriz.
Programa de la serie Fibonacci (sin implicar ningún bucle)
public class Fibonaccifunction
(
private static int indexvalue = 0;
private static int endPoint = 9;
public static void main (String() args)
(
int number1 = 0;
int number2 = 1;
fibonaccifunction(number1, number2);
)
public static void fibonaccifunction(int number1, int number2)
(
System.out.println("index value : " + indexvalue + " -> " + number1);
if (indexvalue == endPoint)
return;
indexvalue++;
fibonaccifunction(number2, number1+number2);
)
)
Salida:
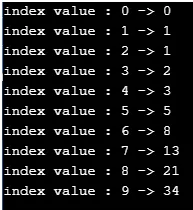
Explicación: implica la lógica del programa redactada anteriormente, pero en este caso, las entradas de Fibonacci se manejan de forma recursiva utilizando una función llamada Fibonacci.
Programa de la serie Fibonacci (sin implicar ningún bucle, pero logrado solo usando condiciones)
public class Fibonacci_with_conditions
(
static int number2=1;
static int number1=0;
static int next=0;
public static void Fibonacci_conditions( int number)
(
if(number<10)
(
if(number == 0)
(
System.out.print(" "+number);
number++;
Fibonacci_conditions (number);
)
else
if(number == 1)
(
System.out.print(" "+number);
number++;
Fibonacci_conditions(number);
)
else(
next=number1+number2;
System.out.print(" "+next);
number1=number2;
number2=next;
number++;
Fibonacci_conditions(number);
)
)
)
public static void main(String() args)
(
Fibonacci_conditions(0);
)
)
Salida:

Explicación: implica la lógica del programa redactada anteriormente, pero en este caso, las entradas de Fibonacci se regulan solo a través de declaraciones condicionales necesarias. Según las condiciones, el intercambio de las variables se realiza necesariamente.
Programa de la serie Fibonacci (sin bucles, los conceptos de bucle se logran utilizando el método nextint)
import java.util.*;
public class Fibonacci_series
(
public static void main(String() args)
(
System.out.println("Input:");
int number= 10, value1=1, value2=0, value3=0;
num(number, value1, value2, value3);
)
public static void num(int number, int value1, int value2, int value3)
(
if(value1 <= number)
(
System.out.println(value1);
value3=value2;
value2=value1;
value1=value2+value3;
num(number, value1, value2, value3);
)
)
)
Salida:
Explicación: Implica la lógica del programa redactada anteriormente, pero en este caso, las entradas de Fibonacci se manejan recursivamente usando una función llamada num y el bucle llevado a cabo usando la función nextInt.
Conclusión - Serie Fibonacci en Java
Estos programas están implicados para lograr la serie de Fibonacci para un valor entero dado. Un conjunto de técnicas en gran medida clasificadas está implícito en la lista de ejemplos dada. Técnicas como un enfoque orientado a matrices y un enfoque de condición sola son muy peculiares.
Artículos recomendados
Esta es una guía de la serie Fibonacci en Java. Aquí discutimos la serie de Fibonacci y un conjunto de técnicas que están implícitas en la lista de ejemplos dada. También puede consultar el siguiente artículo para obtener más información:
- Serie Fibonacci en C
- Matrices 3D en Java
- Anotaciones Java
- StringBuffer en Java
- Herramientas de implementación de Java
- Matrices 3D en C ++
- Generador de números aleatorios en Matlab
- Generador de números aleatorios en C #
- Generador de números aleatorios en JavaScript