
Introducción a la distribución binomial en R
Este artículo describe cómo usar distribuciones binomiales en R para las pocas operaciones involucradas con distribuciones de probabilidad. Business Analysis hace uso de la probabilidad binomial para un problema complejo. R tiene numerosas funciones incorporadas para calcular distribuciones binomiales utilizadas en interferencia estadística. La distribución binomial también conocida como ensayos de Bernoulli toma dos tipos de éxito p y fracaso S. El objetivo principal del modelo de distribución binomial es que calculen los posibles resultados de probabilidad al monitorear un número específico de posibilidades positivas al repetir el proceso un número particular de veces . Deben tener dos resultados posibles (éxito / fracaso), por lo tanto, el resultado es dicotómico. La notación matemática predefinida es p = éxito, q = 1-p.
Hay cuatro funciones asociadas con las distribuciones binomiales. Son dbinom, pbinom, qbinom, rbinom. La sintaxis formateada se da a continuación:
Sintaxis
- dbinom (x, tamaño, problema)
- pbinom (x, tamaño, problema)
- qbinom (x, size, prob) o qbinom (x, size, prob, lower_tail, log_p)
- rbinom (x, tamaño, problema)
La función tiene tres argumentos: el valor x es un vector de cuantiles (de 0 a n), el tamaño es el número de intentos de seguimiento, el problema indica la probabilidad de cada intento. Veamos uno por uno con un ejemplo.
1) dbinom ()
Es una función de densidad o distribución. Los valores del vector deben ser un número entero no deben ser un número negativo. Esta función intenta encontrar una serie de éxitos en un no. de ensayos que son fijos.
Una distribución binomial toma tamaño y valores x. por ejemplo, tamaño = 6, los posibles valores de x son 0, 1, 2, 3, 4, 5, 6, lo que implica P (X = x).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Salida:
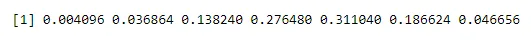
Haciendo probabilidad a uno
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Salida:
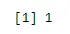
Ejemplo 1 - La base de datos del hospital muestra que los pacientes que padecen cáncer, el 65% muere de él. ¿Cuál será la probabilidad de que de 5 pacientes elegidos al azar de los cuales 3 se recuperen?
Aquí aplicamos la función dbinom. La probabilidad de que 3 se recupere utilizando la distribución de densidad en todos los puntos.
n = 5, p = 0.65, x = 3
dbinom(3, size=5, prob=0.65)
Salida:

Para el valor x de 0 a 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Salida:
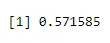
A continuación, cree una muestra de 40 documentos e incremente en 2 también creando binomio usando dbinom.
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
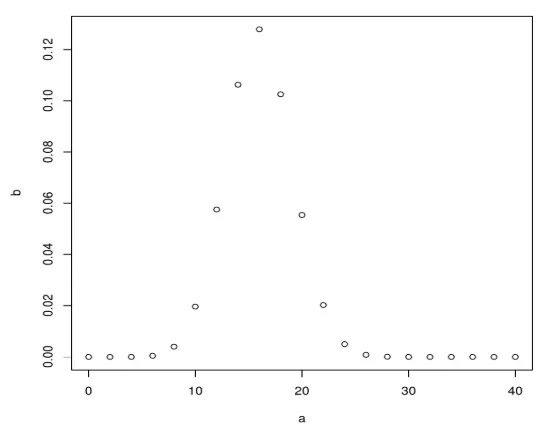
plot(a, b)
Produce el siguiente resultado después de ejecutar el código anterior. La distribución binomial se traza usando la función plot ().
Ejemplo 2: considere un escenario, supongamos que la probabilidad de que un estudiante preste un libro de una biblioteca es 0.7. Hay 6 estudiantes en la biblioteca, ¿cuál es la probabilidad de que 3 de ellos presten un libro?
aquí P (X = 3)
Código:
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
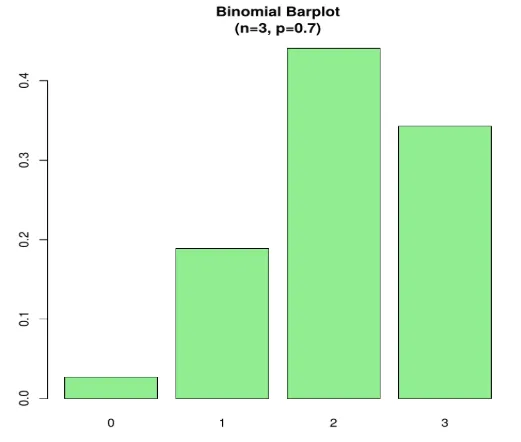
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
La siguiente gráfica muestra cuando p> 0.5, por lo tanto, la distribución binomial está sesgada positivamente como se muestra.
Salida:
2) Pbinom ()
calcula las probabilidades acumulativas de binomio o CDF (P (X <= x)).
Ejemplo 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Salida:

Ejemplo 2: Dravid anota un wicket en el 20% de sus intentos cuando lanza. Si juega 5 veces, ¿cuál sería la probabilidad de que marque 4 o menos wicket?
La probabilidad de éxito es 0.2 aquí y durante 5 intentos obtenemos
pbinom(4, size=5, prob=.2)
Salida:
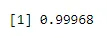
Ejemplo 3: 4% de los estadounidenses son negros. Encuentre la probabilidad de 2 estudiantes negros al seleccionar al azar a 6 estudiantes de una clase de 100 sin reemplazo.
Cuando R: x = 4 R: n = 6 R: p = 0. 0 4
pbinom(4, 6, 0.04)
Salida:-
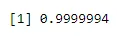
3) qbinom ()
Es una función cuantil y hace lo contrario de la función de probabilidad acumulativa. El valor acumulativo coincide con un valor de probabilidad.
Ejemplo: ¿Cuántas colas tendrán una probabilidad de 0.2 cuando se lanza una moneda 61 veces?
a <- qbinom(0.2, 61, 1/2)
print(a)
Salida:-
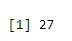
4) rbinom ()
Genera números aleatorios. Diferentes resultados producen diferentes resultados aleatorios, utilizados en el proceso de simulación.
Ejemplo:-
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Salida:-

Cada vez que lo ejecutamos da resultados aleatorios.
rbinom(200, 4, 0.4)
Salida:-

Aquí hacemos esto asumiendo el resultado de 30 lanzamientos de monedas en un solo intento.
rbinom(30, 1, 0.5)
Salida:-
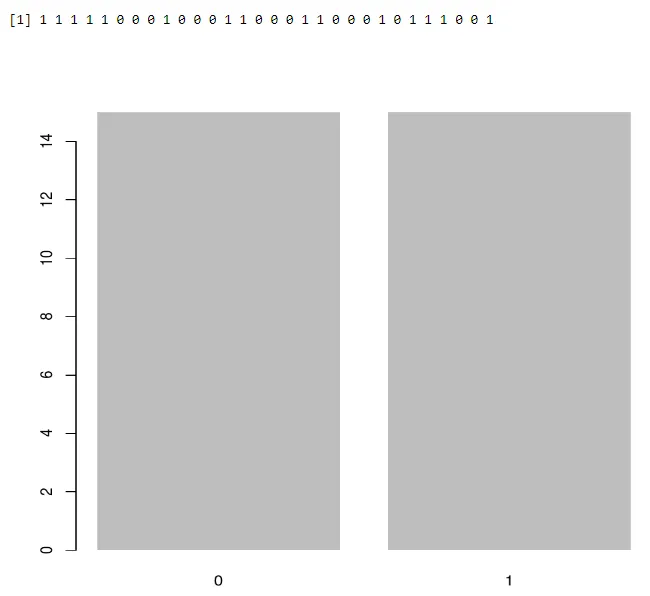
Usando barplot:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Salida:-
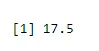
Para encontrar el medio del éxito
output <-rbinom(10, size=60, 0.3)
mean(output)
Salida:-
Conclusión: distribución binomial en R
Por lo tanto, en este documento hemos discutido la distribución binomial en R. Hemos simulado el uso de varios ejemplos en R studio y R snippets y también describimos las funciones incorporadas que ayudan a generar cálculos binomiales. El cálculo de distribución binomial en R usa cálculos estadísticos. Por lo tanto, una distribución binomial ayuda a encontrar probabilidad y búsqueda aleatoria usando una variable binomial.
Artículos recomendados
Esta es una guía para la distribución binomial en R. Aquí hemos discutido una introducción y sus funciones asociadas con la distribución binomial junto con la sintaxis y los ejemplos apropiados. También puede consultar nuestros otros artículos sugeridos para obtener más información:
- Fórmula de distribución binomial
- Economía vs negocios
- Técnicas de análisis de negocios
- Distribuciones de Linux