Introducción a la ordenación del montón en C
La ordenación es una técnica que consiste en ordenar elementos en función de diferentes propiedades. (Propiedades como organizar datos en orden ascendente, descendente o alfabético). Un ejemplo importante de clasificación que podemos pensar aquí es el pedido de artículos durante las compras en línea. Podemos relacionarnos con los precios, la popularidad, las últimas novedades, etc. Por lo tanto, existen muchas técnicas para este posicionamiento de elementos mediante la clasificación. En este tema, vamos a aprender sobre Heap Sort en C.
Aquí vamos a aprender una de las técnicas de clasificación más comunes, Heap Sort, a través del lenguaje de programación C.
La lógica para la ordenación del montón
¿Cómo podemos realmente realizar la ordenación del montón? Veamos a continuación.
En primer lugar, el montón es una de las estructuras de datos basadas en árboles. El árbol involucrado aquí es siempre un árbol binario completo. Y hay dos tipos de montón
- Min - Heap: generalmente organizado en orden ascendente, es decir, si el elemento del nodo primario tiene un valor menor que el de los elementos del nodo secundario.
- Máx. - Montón: generalmente organizado en orden descendente, es decir, si el elemento del nodo primario tiene un valor mayor que el de los elementos del nodo secundario.
Pasos para la ordenación del montón
- Una vez que se obtienen los datos de una lista no ordenada, los elementos se organizan en la estructura de datos del montón, ya sea en base a la creación de un montón mínimo o un montón máximo.
- El primer elemento de la lista anterior se agrega a nuestra matriz
- Nuevamente, se forma la técnica de estructura de datos de cabecera al igual que se sigue el primer paso y nuevamente se recoge el elemento más alto o el menos elemento y se agrega a nuestra matriz.
- Los pasos repetidos nos ayudan a obtener la matriz con la lista ordenada.
Programa para la ordenación del montón en C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Primero, le estamos pidiendo al usuario que ingrese el número de elementos que se toman para ordenar y luego se le permite al usuario ingresar diferentes elementos que se ordenarán.
Pasos seguidos
- Lo siguiente en lo que nos estamos enfocando es crear una matriz de almacenamiento dinámico, en este caso, matriz de almacenamiento dinámico máximo.
- La condición principal para obtener una matriz de almacenamiento dinámico máximo es verificar que ningún valor de nodo primario sea menor que su valor de nodo secundario. Vamos a intercambiar hasta lograr esa condición.
- La principal ventaja de este árbol binario completo es que se puede acceder a los nodos secundarios izquierdo y derecho de un nodo primario con valores 2 (i) + 1 y 2 * (i) + 2 valores respectivamente. Donde i es el nodo padre.
- Entonces, por ese camino aquí, estamos colocando nuestro nodo raíz que contiene el valor máximo en el lugar del nodo hoja más a la derecha. Y luego nuevamente siguiendo el mismo procedimiento, de modo que el siguiente número máximo se convierta en el nodo raíz.
- Vamos a seguir el mismo procedimiento hasta que solo quede un nodo en la matriz de almacenamiento dinámico.
- Y luego, estamos organizando nuestra matriz de montón para formar una matriz ordenada perfecta en orden creciente.
- Finalmente, estamos imprimiendo la matriz ordenada en la salida.
Salida:
La salida se adjunta a continuación.
Déjame mostrarte la representación pictórica de los acontecimientos:
- Los datos ingresados se representan primero en forma de una matriz unidimensional de la siguiente manera.

- La representación pictórica del árbol binario formado es la siguiente:
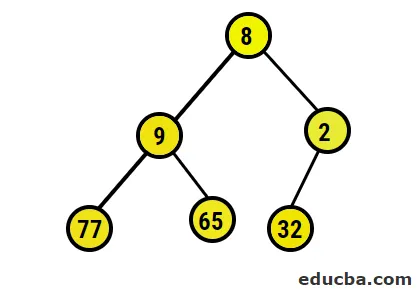
- Ahora, vamos a convertir al montón máximo asegurándonos de que todos los nodos primarios sean siempre mayores que los nodos secundarios. Como se mencionó en la salida en la matriz ordenada de montón, la representación gráfica sería:
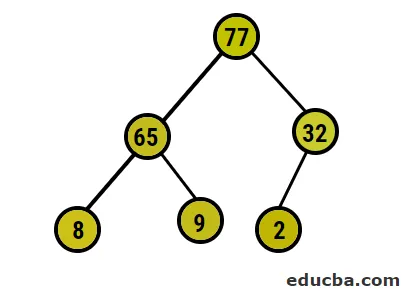
- Después de esto, vamos a intercambiar el nodo raíz con el nodo hoja extremo y luego lo eliminaremos del árbol. El nodo hoja sería la raíz de vez en cuando el mismo proceso e seguido para obtener nuevamente el elemento más alto en la raíz
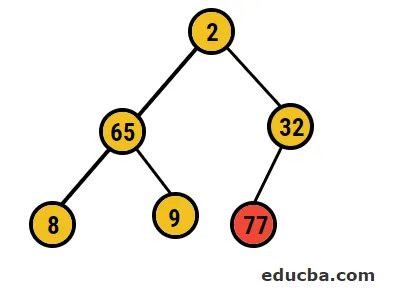
- Entonces, en este caso, se eliminan 77 dígitos de este árbol y se colocan en nuestra matriz ordenada y el proceso se repite.
Lo anterior lo hemos visto para formar max heap array. El mismo proceso se trata con la formación de la matriz min-heap también. Como se discutió anteriormente, la única diferencia es con la relación entre los elementos del nodo primario y secundario.
Como ejercicio, ¿puedes intentar formar el montón en orden descendente?
Conclusión
Aunque hay muchas técnicas de clasificación, la clasificación de montón se considera una de las mejores técnicas de clasificación debido a su complejidad de tiempo y espacio. La complejidad de tiempo para todos los casos mejores, medios y peores es O (nlogn), donde la complejidad del peor caso es mejor que la complejidad del caso más rápido de Quicksort y la complejidad del espacio es O (1).
Artículos recomendados
Esta es una guía de Heap Sort en C. Aquí discutimos la lógica y los Pasos para Heap Sort con el código de muestra y la salida junto con representaciones pictóricas. También puede echar un vistazo a los siguientes artículos para obtener más información:
- Heap Ordenar en Java
- Selección Ordenar en Java
- Palindrome en el Programa C
- Patrones en programación C
- Heap Sort en C ++ (Algoritmo)
- Heap Sort en Python
- C Multiplicación de la matriz de programación