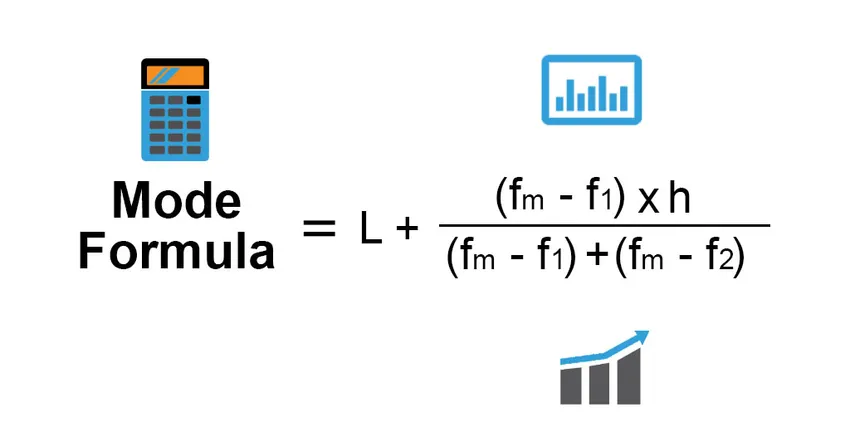
Fórmula de modo - Calculadora (ejemplos con plantilla de Excel)

Fórmula de modo (tabla de contenido)

• Fórmula
• Ejemplos
• Calculadora

¿Qué es la fórmula del modo?

Las tres medidas centrales de tendencia son la media y la moda medias. Cuando los tres se usan juntos para extraer un análisis significativo en el conjunto de datos. Hoy en este artículo discutiremos el modo, que también es una de las claves y el método importante utilizado en la tendencia central. El modo se refiere al valor más frecuente en el conjunto de datos. El modo de un dato se puede encontrar con un conjunto de datos normal, un conjunto de datos grupales y un conjunto de datos no agrupados o no agrupados. Sin embargo, la media que se usa con más frecuencia sigue siendo la mejor medida de tendencia central a pesar de la existencia de la media, la mediana y la moda. En este artículo, intentaremos comprender la función de modo, los ejemplos y las explicaciones de cada ejemplo junto con la fórmula y los cálculos.

La fórmula para el modo es: -

Mode = L + (fm−f1)h /(fm−f1)+(fm−f2)

Fórmula de modo para datos agrupados:

Modo = L + (fm − f1) h / 2fm − f1 − f2

Dónde,

• L = Modo límite inferior de la clase modal
• fm = frecuencia de la clase modal
• f1 = Frecuencia de clase que precede a la clase modal
• f2 = Frecuencia de clase que sucede a la clase modal
• h = Tamaño del intervalo de clase

Ejemplos de fórmula de modo (con plantilla de Excel)

Tomemos un ejemplo para comprender el cálculo del modo de una mejor manera.

Puede descargar esta plantilla de Excel de fórmula de modo aquí - Plantilla de Excel de fórmula de modo

Fórmula de modo - Ejemplo # 1

Donde el modo se calcula simplemente el número de observaciones en un conjunto de datos que ocurre la mayor parte del tiempo.

Calcule el modo del siguiente conjunto de datos.

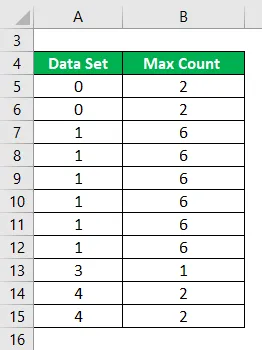
Solución:

Un modo se calcula como:

Número de observaciones en un conjunto de datos que ocurre la mayor parte del tiempo

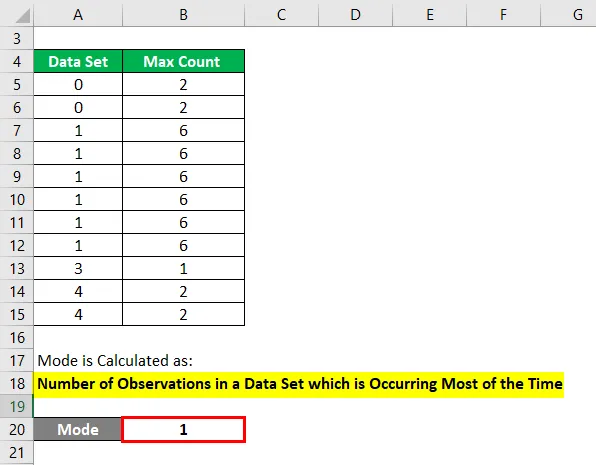
• Modo = 1

Fórmula de modo - Ejemplo # 2

Calcule el modo utilizando la información dada.

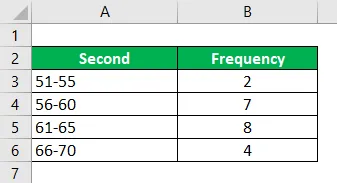
Solución:

Nota: - Primero, el grupo modal con la frecuencia más alta necesita identificar Si el intervalo no es continuo, 0.5 debe sustraerse del Modo límite inferior y 0.5 debe agregarse del Modo límite superior. Entonces el intervalo será

El grupo modal se calcula como:

Grupo modal que es más frecuente, es decir, 60.5-65.5

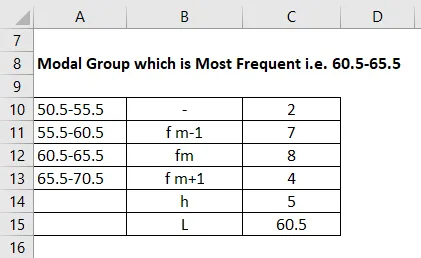
Entonces la frecuencia más baja es del grupo modal que es 4, en este caso, se toma como fm + 1 y fm-1 se convertirá en 7 en este ejemplo. Y tenemos fm que es la frecuencia como 8. El (h) se llama El tamaño del intervalo de clase es 5, que también tenemos en cuenta el intervalo de inicio. L es 60.5.

El modo se calcula utilizando la fórmula dada a continuación

Modo = L + (fm − f1) h / (fm − f1) + (fm − f2)

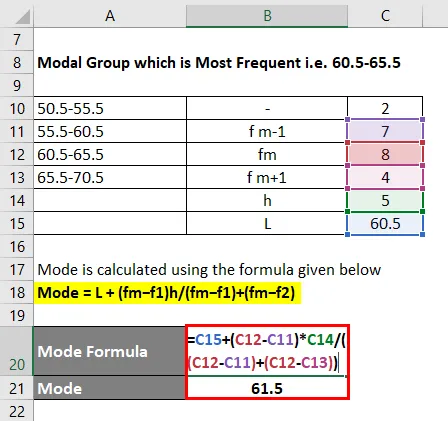
• Modo = 60.5 + (8 - 7) * 5 / ((8 - 7) + (8 - 4))
• Modo = 61.5

Fórmula de modo - Ejemplo # 3

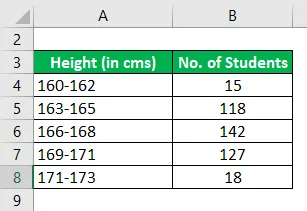
Las siguientes son las distribuciones de alturas en una determinada clase de estudiantes en un modo determinado

Calcule el modo utilizando la información dada.

Solución:

Si el intervalo no es continuo, se debe restar 0.5 del modo de límite inferior y se debe agregar 0.5 del modo de límite superior. Entonces el intervalo será

El grupo modal se calcula como:

Grupo modal que es más frecuente, es decir, 165.5-168.5

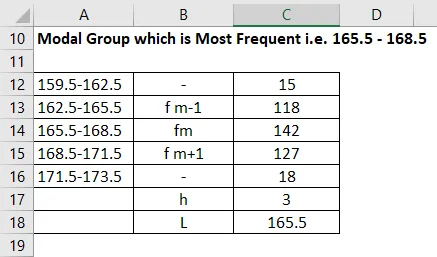
El modo se calcula utilizando la fórmula que figura a continuación.

Modo = L + (fm − f1) h / (fm − f1) + (fm − f2)

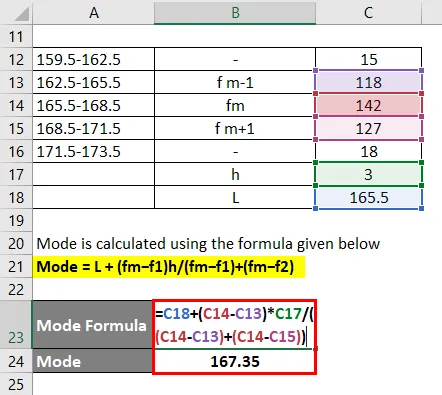
• Modo = 165.5 + (142 - 118) * 3 / (142 - 118) + (142 - 127)
• Modo = 167.35

Explicación

El modo puede explicarse simplemente como el valor que ocurre con mayor frecuencia en el conjunto de datos. Y el modo anterior puede explicarse como cuando los datos son un grupo, primero necesitamos calcular la función modal y también hacer que los datos sean continuos para calcular el modo de los datos. La clase modal se decide con la clase que tiene la frecuencia más alta en el conjunto de datos.

Relevancia y usos de la fórmula del modo

• La media, la mediana y la moda revelan diferentes aspectos de sus datos. Cualquiera le dará una idea general, pero puede confundirlo; tener los tres te dará una imagen más completa
• Para una distribución normal, el modo, la media y la mediana tienen el mismo valor, ya que el Modo es una distribución normal. El modo de análisis aislado no refleja la imagen real, si desea analizar el conjunto de datos completo, entonces las tres medidas estadísticas deben analizarse en detalle e interpretarse
• El modo es fácil de entender y simple de calcular.
• El modo no se ve afectado por valores extremadamente grandes o pequeños.
• El modo puede ubicarse simplemente mediante inspección en datos no agrupados y distribución de frecuencia discreta.
• El modo puede ser útil para datos cualitativos.
• El modo se puede calcular en una tabla de frecuencia abierta.
• El modo se puede ubicar gráficamente
• El modo es usado por los científicos de datos más comúnmente
• El modo es que no nos proporcionará una muy buena medida de tendencia central cuando la marca más común está lejos del resto de los datos en el conjunto de datos

Calculadora de fórmula de modo

Puede usar la siguiente calculadora de fórmulas de modo

L
fm
f1
f2
h
Fórmula de modo

Fórmula de modo =	L + (fm - f1) xh / (fm - f1) + (fm - f2)
=	0 + (0-0) x 0 / (0-0) + (0-0) = 0

Artículos recomendados

Esta es una guía para la fórmula de modo. Aquí discutimos cómo calcular la fórmula del modo junto con ejemplos prácticos. También proporcionamos una calculadora de modo con una plantilla de Excel descargable. También puede consultar los siguientes artículos para obtener más información:

1. Ejemplos de la fórmula del modelo de crecimiento Gordon
2. Fórmula para calcular el modelo de precios de activos de capital
3. Calculadora para fórmula de relación de gastos totales
4. Fórmula de distribución de Poisson (ejemplos con plantilla de Excel)