Introducción a las matrices 2-D en C
Una matriz es un grupo de elementos con el mismo tipo de datos (homogéneo). También se llama un tipo de datos Derivado. Si consideramos un tipo de datos primitivo y asignamos un valor como se muestra a continuación,
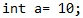
Y ahora, si queremos almacenar un nuevo valor en la variable a, el nuevo valor reemplaza al antiguo. Usando una variable primitiva podemos almacenar solo un valor a la vez, no podemos almacenar múltiples valores.
Para almacenar más de un elemento en una sola variable, como las marcas de los estudiantes, los identificadores de los empleados, los números móviles con una gran cantidad de datos, tenemos que crear cientos de variables únicas, lo cual es una tarea muy compleja. Por eso se introdujo el concepto de matrices.
Conceptos en matrices 2-D en C
Podemos definir matrices en
- Unidimensional
- Doble dimensión
Y así sucesivamente hasta N-Dimensional según el requisito. Pero aquí vamos a tratar con matrices 2-D. Como su nombre indica, las matrices en 2-D pueden ser una representación matricial de datos, que se crean para implementar una estructura de datos similar a una base de datos relacional y se pueden almacenar en forma de tabla. Proporciona facilidad para mantener los datos masivos que se pueden pasar a cualquier número de funciones según el requisito. Se puede acceder a los datos en estas matrices a través de los identificadores de fila y columna.
¿Cómo podemos definirlos e implementarlos? ¿Dónde podemos usarlos? Yendo más allá, comprendamos esos conceptos.
En C, las matrices dimensionales se pueden declarar de la siguiente manera:
Sintaxis
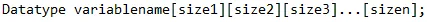
Entonces, de la misma manera, podemos declarar la matriz 2-D como:
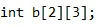
El significado de la representación anterior se puede entender como:
- La memoria asignada a la variable b es del tipo de datos int.
- Los datos se representan en forma de 2 filas y 3 columnas.

Se puede acceder a los datos dentro de la matriz a través de la representación anterior. En la representación de matrices en 2-D, el primer corchete representa el número de filas, y el segundo es para el número de columnas. La representación de índice de la matriz para el primer elemento siempre comienza con cero y termina con tamaño-1. La variable de matriz (aquí b) siempre contiene la dirección base del bloque de memoria y se denomina variable de puntero interno.
Entonces, por ejemplo, si el número de filas es 3, entonces la representación del índice para acceder a los datos en las filas será 0, 1 y 2. La misma lógica se aplica también a los índices de columna. Para la representación anterior, para obtener los datos de la 2da fila 3ra columna, podemos acceder por b (1) (2).
Inicializando matrices
Tenemos dos métodos diferentes para inicializar los valores en C. Los métodos solo difieren sintácticamente.
Debajo está uno de ellos.

Otra forma de inicializar es la siguiente:
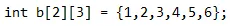
Generalmente, se prefiere el primer método de inicialización ya que podemos entender y visualizar claramente las filas y columnas de las matrices 2-D en C.
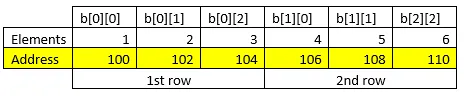
A continuación se muestra el ejemplo de la representación gráfica de los elementos y su dirección para la matriz b.
Los elementos de una matriz generalmente se almacenan en ubicaciones de memoria consecutivas en función del tipo de datos de los elementos.
Insertar elementos en matrices 2-D
Para insertar elementos en matrices 2-D, necesitamos insertar los datos tanto en filas como en columnas. Entonces, para esto, utilizamos el concepto de bucles. En el proceso anterior para inicializar los datos en una matriz, habíamos predefinido los valores.
Aquí, los elementos pueden ser insertados dinámicamente por el usuario, según los requisitos. A continuación se muestra un código de ejemplo para insertar los elementos.
#include
int main()
(
int b(2)(3);
int i, j, num;
printf("Enter elements into 2-D array: ");
for(i=0;i<2;i++)
(
for(j=0;j<3;j++)
(
scanf("%d", &b(i)(j));
)
)
)
Como se observa en el código:
- Primero, declaramos la variable de matriz y las dimensiones de la matriz con el número de filas y columnas.
- Luego declaramos dos variables para iterar sobre los elementos de la matriz.
- Luego, para bucles se utilizan. El bucle externo es para la iteración de filas y el bucle interno es para las columnas.
- La función Scanf se usa para leer los datos a medida que ingresamos, y luego coloca el valor insertado en esas posiciones de i y j.
En el ejemplo anterior, insertamos los datos en una matriz que tiene 2 filas y 3 columnas. El resultado de lo siguiente se puede obtener de la siguiente manera:

Como no hemos utilizado la función printf para mostrar la salida, el programa escrito solo había leído los valores ingresados por el usuario. Después de escribir la función de impresión (utilizando bucles for), la salida se mostrará como:
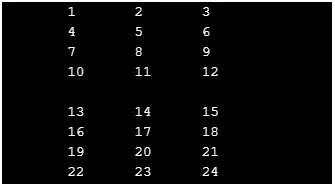
Actualizar elementos en matrices 2-D
La actualización de elementos en una matriz se puede hacer ya sea especificando un elemento en particular para ser reemplazado o identificando una posición donde se debe hacer el reemplazo. Para la actualización, generalmente requerimos los siguientes detalles.
- Elementos de una matriz.
- Posición / elemento, donde debe insertarse
- El valor a insertar.
Para actualizar los datos en una matriz a través de los detalles del elemento, primero debemos buscar ese elemento en la matriz, comprender su posición y luego reemplazar el elemento antiguo con el nuevo elemento.
Aquí, hemos dado a continuación dos ejemplos de actualización del elemento de una matriz 2-D.
En primer lugar, veamos un ejemplo en el que ya se conoce la posición del elemento a actualizar.
#include
int main()
(
int b(2)(3);
int i, j, num;
printf("Enter elements into 2-D array: ");
for(i=0;i<2;i++)
(
for(j=0;j<3;j++)
(
scanf("%d", &b(i)(j));
)
)
b(0)(2)=10;
for(i=0;i<2;i++)
(
for(j=0;j<3;j++)
(
printf("\t%d", b(i)(j));
)
printf("\n");
)
return 0;
)
En el programa anterior, se selecciona el elemento en la 1ra fila y la 3ra columna y se actualiza el valor de los datos en esa posición.
La salida de arriba es la siguiente:

En el segundo ejemplo, vamos a mostrar cómo la posición del elemento puede tomarse dinámicamente como un valor ingresado por el usuario y actualizar el valor del elemento en esa posición en particular.
#include
int main()
(
int b(2)(3);
int i, j, num;
printf("Enter elements into 2-D array: ");
for(i=0;i<2;i++)
(
for(j=0;j<3;j++)
(
scanf("%d", &b(i)(j));
)
)
printf("Enter the value of row and coulmn number :");
scanf("%d %d", &i, &j);
printf("Enter the number you want to update with: ");
scanf("%d", &num);
b(i)(j)=num;
for(i=0;i<2;i++)
(
for(j=0;j<3;j++)
(
printf("\t%d", b(i)(j));
)
printf("\n");
)
return 0;
)
Aquí, utilizamos la función scanf para leer el valor dado por el usuario según su elección para la posición de un elemento basado en números de fila y columna.
La salida es la siguiente:
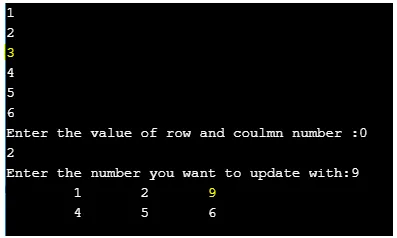
Como ejercicio, ¿puede intentar escribir un programa para actualizar toda la fila de la matriz con valores ingresados por el usuario?
Ahora, como sabemos, en la matriz 2-D, declaramos el tamaño de la matriz al principio. Somos conscientes del tamaño de la matriz, pero ¿qué sucede si el usuario da un número aleatorio de fila y columna fuera de nuestro tamaño de matriz?

Tenga en cuenta que, como no habíamos escrito ninguna condición if / else o try / catch, la salida de la matriz no cambia. Sin embargo, podemos escribir el código utilizando las condiciones mencionadas anteriormente para mostrar errores en tales casos.
Eliminar elementos en matrices 2-D
Después de los conceptos de inserción y actualización de los datos dentro de la matriz, veamos ahora cómo podemos eliminar una fila completa de la matriz.
Hemos escrito un programa en un formato simple para que se pueda entender fácilmente el concepto de diferentes operaciones en una matriz de 2-d.
#include
int main()
(
int b(2)(3), i, j, num, x;
printf("Enter elements into 2-D array: ");
for(i=0;i<2;i++)
(
for(j=0;j<3;j++)
(
scanf("%d", &b(i)(j));
)
)
printf("Enter the value of row number :");
scanf("%d", &x);
for(i=0;i<2;i++)
(
if(i==x)
(
for(j=0;j<3;j++)
(
if((i+1)<2)
(
printf("\t%d", b(i+1)(j));
)
)
i++;)
else
(
for(j=0;j<3;j++)
(
printf("\t%d", b(i)(j));
)
)
printf("\n");
)
)
Los pasos seguidos son:
- Tomó los valores de una matriz dinámicamente
- Pidió al usuario que ingrese el número (índice) de la fila que debe eliminarse.
- Utilizando la iteración de bucle, estamos comparando si el número de fila y el número de entrada del usuario coinciden o no.
- Si coinciden y el número de fila es menor que el tamaño de una matriz, estamos imprimiendo la siguiente fila. De lo contrario, estamos imprimiendo la fila tal como está.
La salida es la siguiente:
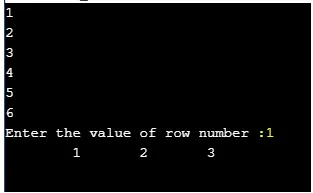
¿Qué sucede si doy el número de fila fuera del límite de la matriz?

No encontrará la fila para eliminar y salir del programa imprimiendo toda la matriz.
Como ya se sabe, incluso podemos declarar los valores de los números de fila y columna dinámicamente y escribir el programa en consecuencia.
¿No parece esto simple y fácil de aprender?
Como ejercicio, ¿puede intentar eliminar un elemento particular para la matriz 2-d ahora?
Conclusión
En esta sección, hemos aprendido las operaciones básicas en matrices bidimensionales. Estas matrices en 2-d son útiles en tiempo real con las operaciones matriciales y muchos cálculos matemáticos.
Las matrices incluso se pueden usar para mostrar calendarios, ubicaciones del estacionamiento, e incluso podemos tener un juego de ajedrez.
Muchas otras estructuras de datos como Listas vinculadas, Cola, Gráficos, Árboles tienen que usar este concepto de matrices 2-D como requisito básico para almacenar y acceder a las ubicaciones de diferentes elementos. Intenta resolver las operaciones básicas de las matrices 2D y diviértete aprendiendo C.
Artículos recomendados
Esta es una guía de matrices 2-D en C. Aquí discutimos la introducción, inicialización de matrices, inserción, actualización, eliminación de elementos en matrices 2-D. También puede consultar los siguientes artículos para obtener más información:
- Arreglos en R
- Ventajas de la matriz
- Matrices en C ++
- Matrices en JavaScript
- Ejemplos de matrices en C #
- Matrices en PHP