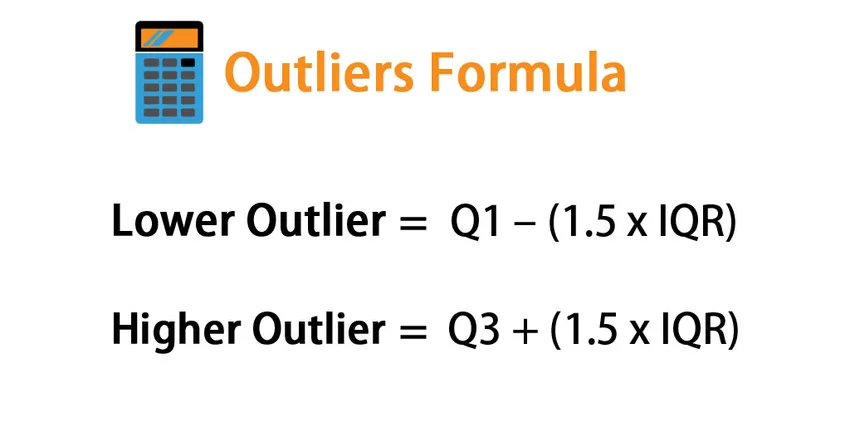
Fórmula de valores atípicos (Tabla de contenido)
- Fórmula de valores atípicos
- Ejemplos de fórmula de valores atípicos (con plantilla de Excel)
Fórmula de valores atípicos
En estadística, los valores atípicos son los dos puntos inusuales distanciados extremos en los conjuntos de datos dados. El valor extremadamente alto y los valores extremadamente bajos son los valores atípicos de un conjunto de datos. Esto es muy útil para encontrar cualquier falla o error que haya ocurrido. Simplemente como su nombre lo dice, los valores atípicos son valores que se encuentran fuera del resto de los valores en el conjunto de datos. Ejemplo, considere a los estudiantes de ingeniería e imagine que tenían enanos en su clase. Entonces, los enanos son las personas que tienen una altura extremadamente baja en comparación con otras personas normales. Entonces este es el valor atípico en esta clase. Los valores atípicos se pueden calcular utilizando el método de Tukey.
La fórmula para los valores atípicos:
Lower Outlier = Q1 – (1.5 * IQR)
Higher Outlier= Q3 + (1.5 * IQR)
Ejemplos de fórmula de valores atípicos (con plantilla de Excel)
Tomemos un ejemplo para comprender el cálculo de la fórmula Outliers de una mejor manera.
Puede descargar esta plantilla de valores atípicos aquí - Plantilla de valores atípicosFórmula de valores atípicos - Ejemplo # 1
Considere el siguiente conjunto de datos y calcule los valores atípicos para el conjunto de datos.
Conjunto de datos = 5, 2, 7, 98, 309, 45, 34, 6, 56, 89, 23
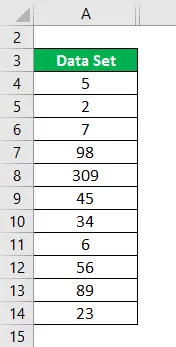
Orden ascendente del conjunto de datos:
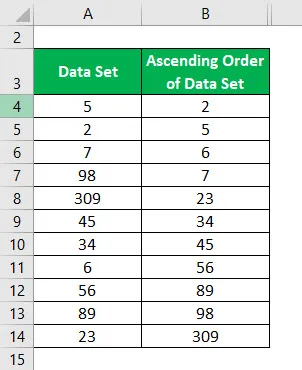
La mediana del conjunto de datos de orden ascendente se calcula como:
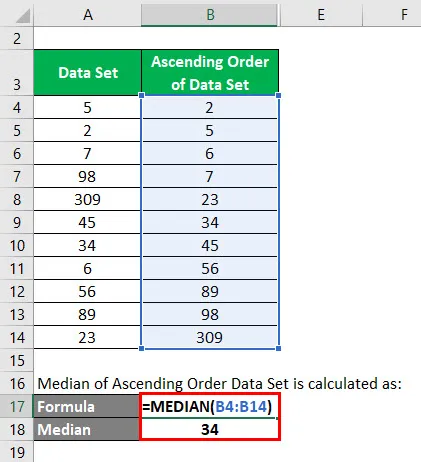
En este conjunto de datos, el número total de datos es 11. Entonces n = 11. Mediana = 11 + 1/2 = 12/2 = 6. Por lo tanto, el valor que está en la 6ª posición en este conjunto de datos es la mediana.
Entonces el valor medio = 34.
Divida el conjunto de datos en 2 mitades usando la mediana.
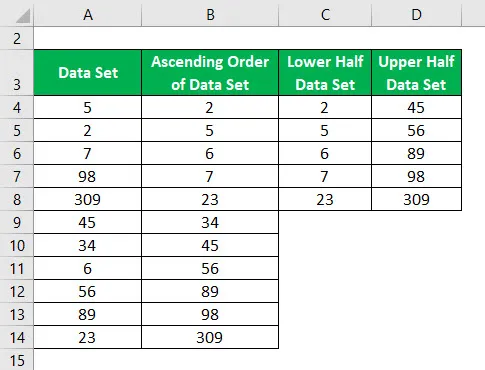
La mediana del conjunto de datos de la mitad inferior y la mitad superior se calcula como:
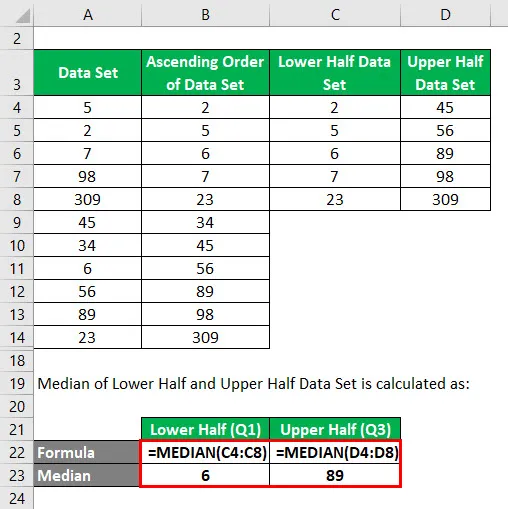
- En la mitad inferior 2, 5, 6, 7, 23, si encontramos la mediana como la encontramos en el paso 2, el valor medio sería 6. Entonces Q1 = 6.
- En la mitad superior 45, 56, 89, 98, 309 si encontramos la mediana como la encontramos en el paso 2, el valor medio sería 89. Entonces Q3 = 89.
IQR se calcula utilizando la fórmula que se proporciona a continuación
IQR = Q3 - Q1
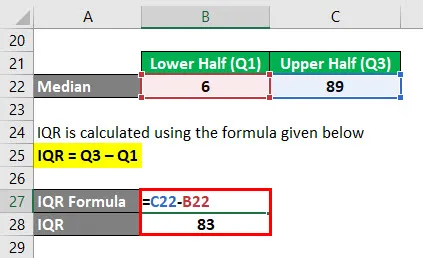
- IQR = 89 -6
- IQR = 83
El valor atípico inferior se calcula utilizando la fórmula que se proporciona a continuación
Outlier inferior = Q1 - (1.5 * IQR)
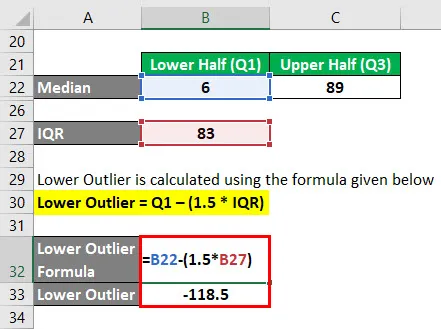
- Outlier inferior = 6 - (1.5 * 83)
- Outlier inferior = -118.5
Mayor valor atípico se calcula utilizando la fórmula que se proporciona a continuación
Mayor valor atípico = Q3 + (1.5 * IQR)
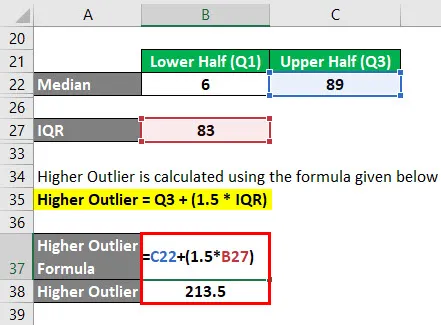
- Mayor valor atípico = 89 + (1.5 * 83)
- Mayor valor atípico = 213.5
Ahora busque estos valores en el conjunto de datos -118.5, 2, 5, 6, 7, 23, 34, 45, 56, 89, 98, 213.5, 309. Valores que caen por debajo en el valor del lado inferior y arriba en el lado superior son el valor atípico. Para este conjunto de datos, 309 es el valor atípico.
Fórmula de valores atípicos - Ejemplo # 2
Considere el siguiente conjunto de datos y calcule los valores atípicos para el conjunto de datos.
Conjunto de datos = 45, 21, 34, 90, 109.
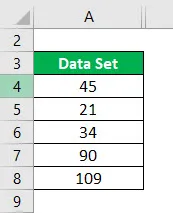
Orden ascendente del conjunto de datos:
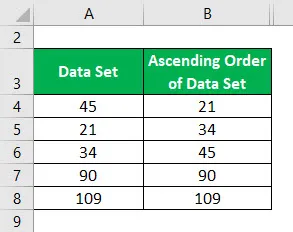
La mediana del conjunto de datos de orden ascendente se calcula como:
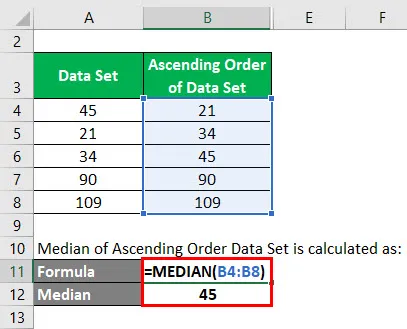
En este conjunto de datos, el número total de datos es 5. Entonces n = 5. Mediana = 5 + 1/2 = 6/2 = 3. Por lo tanto, el valor que está en la tercera posición en este conjunto de datos es la mediana.
Entonces el valor medio = 45.
Divida el conjunto de datos en 2 mitades usando la mediana.
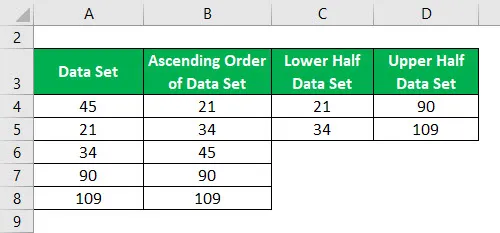
La mediana del conjunto de datos de la mitad inferior y la mitad superior se calcula como:
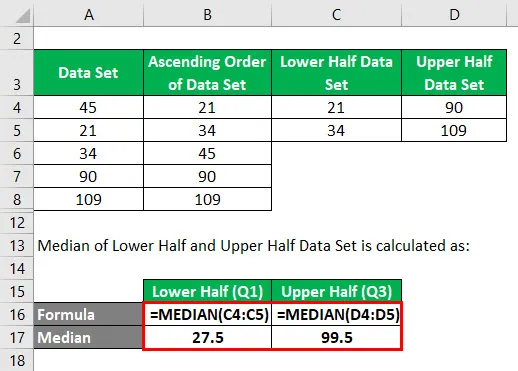
- Q1 = 27.5
- Q3 = 89
IQR se calcula utilizando la fórmula que se proporciona a continuación
IQR = Q3 - Q1
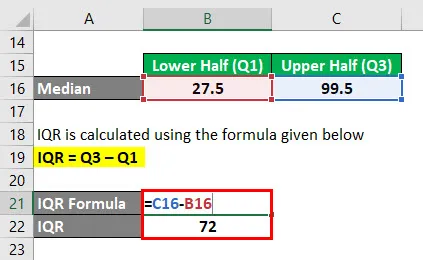
- IQR = 99.5 - 27.5
- IQR = 72
El valor atípico inferior se calcula utilizando la fórmula que se proporciona a continuación
Outlier inferior = Q1 - (1.5 * IQR)
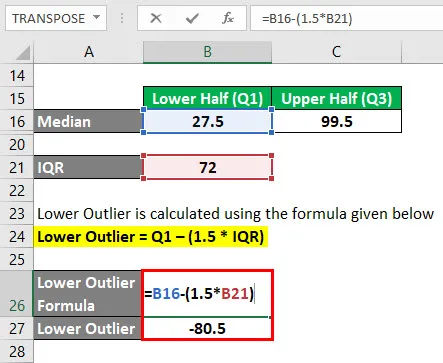
- Outlier inferior = 27.5 - (1.5 * 72)
- Outlier inferior = -80.5
Mayor valor atípico se calcula utilizando la fórmula que se proporciona a continuación
Mayor valor atípico = Q3 + (1.5 * IQR)
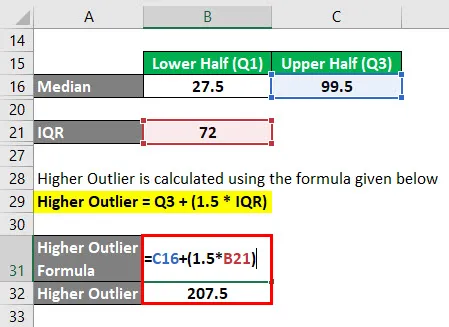
- Mayor valor atípico = 99.5 + (1.5 * 72)
- Mayor valor atípico = 207.5
Explicación
Paso 1: Organice todos los valores en el conjunto de datos dado en orden ascendente.
Paso 2: encuentre el valor medio para los datos que se ordenan. La mediana se puede encontrar usando la siguiente fórmula. El siguiente cálculo simplemente le da la posición del valor medio que reside en la fecha establecida.
Mediana = (n + 1) / 2
Donde n es el número total de datos disponibles en el conjunto de datos.
Paso 3: Encuentre el valor inferior del cuartil Q1 del conjunto de datos. Para encontrar esto, el uso del valor medio divide el conjunto de datos en dos mitades. Del medio conjunto de valores inferior, encuentre la mediana para ese conjunto inferior, que es el valor Q1.
Paso 4: Encuentre el valor del cuartil superior Q3 del conjunto de datos. Es exactamente como el paso anterior. En lugar de la mitad inferior, tenemos que seguir el mismo procedimiento que la mitad superior del conjunto de valores.
Paso 5: Encuentre el valor del rango intercuartil IQR. Para encontrar el valor de Deducir Q1 de Q3.
IQR = Q3-Q1
Paso 6: Encuentra el valor Inner Extreme. Un final que cae fuera del lado inferior que también se puede llamar como un valor atípico menor. Multiplique el valor IQR por 1.5 y deduzca este valor de Q1 para obtener el extremo Inner Lower.
Outlier inferior = Q1 - (1.5 * IQR)
Paso 7: Encuentre el valor extremo externo. Un final que cae fuera del lado superior, que también se puede llamar un valor atípico importante. Multiplique el valor de IQR por 1.5 y sume este valor con Q3 para obtener el extremo superior externo.
Mayor valor atípico = Q3 + (1.5 * IQR)
Paso 8: Los valores que quedan fuera de estos extremos internos y externos son los valores atípicos para el conjunto de datos dado.
Relevancia y usos de la fórmula de valores atípicos
Los valores atípicos son muy importantes en cualquier problema de análisis de datos. Outlier muestra inconsistencia en cualquier conjunto de datos, ya que se define como los valores distantes poco comunes en el conjunto de datos de uno a otro. Esto es muy útil para encontrar fallas que ocurrieron en el conjunto de datos. Porque cuando coloca un error en el conjunto de datos, afecta la media y la mediana, por lo tanto, puede obtener grandes desviaciones en el resultado si los valores atípicos están en el conjunto de datos. Por lo tanto, es esencial descubrir valores atípicos del conjunto de datos para evitar problemas serios en el análisis estadístico.
Artículos recomendados
Esta ha sido una guía para la fórmula de valores atípicos. Aquí discutimos cómo calcular valores atípicos junto con ejemplos prácticos y plantillas de Excel descargables. También puede consultar los siguientes artículos para obtener más información:
- Guía para la fórmula de rango medio
- Ejemplos de fórmula salarial
- Calculadora para fórmula DPMO
- ¿Cómo calcular la distribución T?
- Fórmula de desviación del cuartil | Ejemplos