
Introducción al algoritmo DFS
DFS se conoce como el algoritmo de búsqueda de profundidad primero que proporciona los pasos para atravesar todos y cada uno de los nodos de un gráfico sin repetir ningún nodo. Este algoritmo es el mismo que el primer recorrido de profundidad para un árbol, pero difiere en mantener un valor booleano para verificar si el nodo ya ha sido visitado o no. Esto es importante para el recorrido del gráfico ya que también existen ciclos en el gráfico. Se mantiene una pila en este algoritmo para almacenar los nodos suspendidos durante el recorrido. Se llama así porque primero viajamos a la profundidad de cada nodo adyacente y luego continuamos atravesando otro nodo adyacente.
Explicar el algoritmo DFS
Este algoritmo es contrario al algoritmo BFS donde se visitan todos los nodos adyacentes seguidos de vecinos a los nodos adyacentes. Comienza a explorar el gráfico desde un nodo y explora su profundidad antes de retroceder. Se consideran dos cosas en este algoritmo:
- Visitar un vértice: selección de un vértice o nodo del gráfico para atravesar.
- Exploración de un vértice: atravesar todos los nodos adyacentes a ese vértice.
Pseudocódigo para la profundidad de la primera búsqueda :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
El recorrido lineal también existe para DFS que se puede implementar de 3 maneras:
- Hacer un pedido
- En orden
- Orden de publicación
El postorder inverso es una forma muy útil de atravesar y se utiliza en la clasificación topológica, así como en diversos análisis. También se mantiene una pila para almacenar los nodos cuya exploración aún está pendiente.
Gráfica transversal en DFS
En DFS, se siguen los siguientes pasos para recorrer el gráfico. Por ejemplo, un gráfico dado, comencemos el recorrido desde 1:
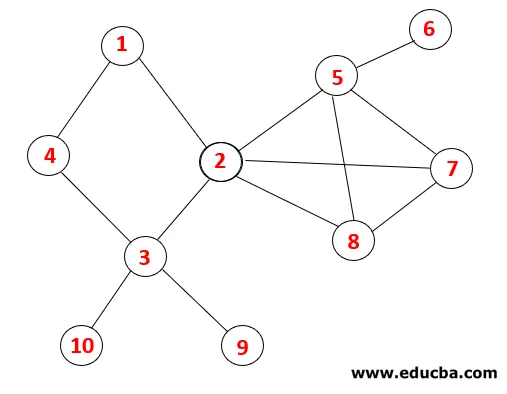
| Apilar | Secuencia transversal | Árbol de expansión |
| 1 |  |
|
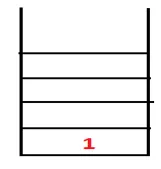 | 1, 4 |  |
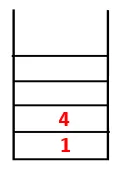 | 1, 4, 3 |  |
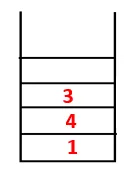 | 1, 4, 3, 10 | 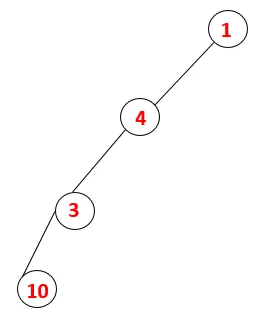 |
 | 1, 4, 3, 10, 9 | 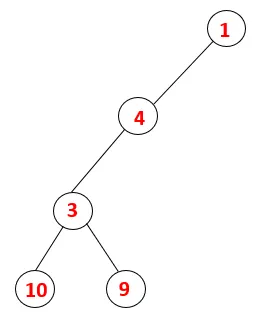 |
 | 1, 4, 3, 10, 9, 2 | 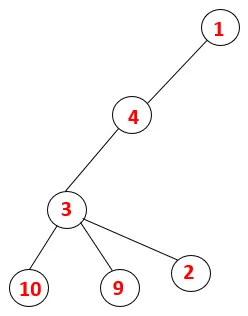 |
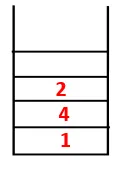 | 1, 4, 3, 10, 9, 2, 8 |  |
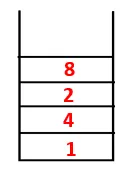 | 1, 4, 3, 10, 9, 2, 8, 7 | 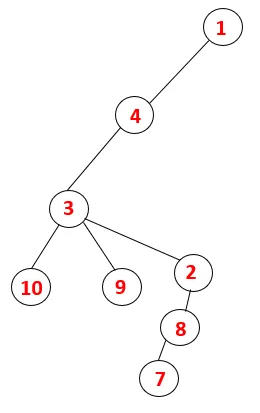 |
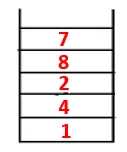 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
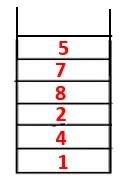 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 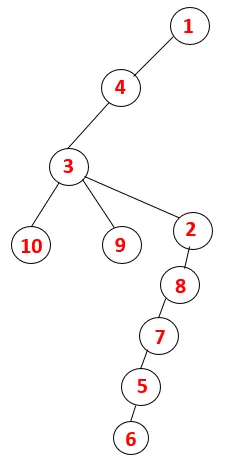 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 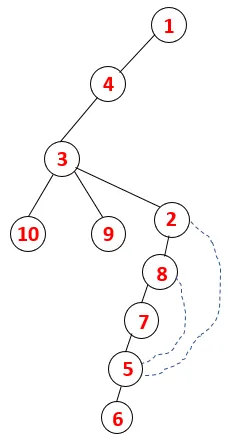 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 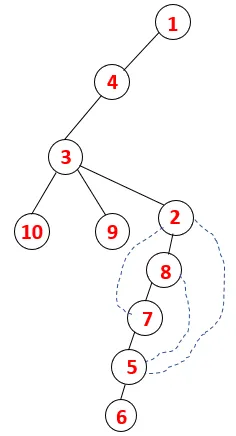 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 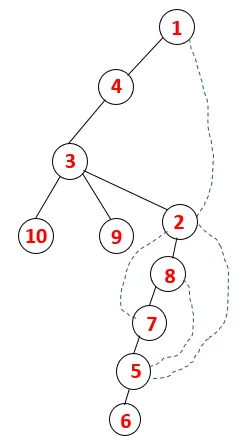 |
Explicación al algoritmo DFS
A continuación se detallan los pasos para el algoritmo DFS con ventajas y desventajas:
Paso 1: se visita el nodo 1 y se agrega a la secuencia, así como al árbol de expansión.
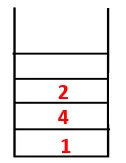
Paso 2: se exploran los nodos adyacentes de 1 que son 4, por lo tanto, 1 se empuja a la pila y 4 se empuja a la secuencia, así como al árbol de expansión.
Paso 3: se explora uno de los nodos adyacentes de 4 y, por lo tanto, 4 se empuja a la pila, y 3 ingresa a la secuencia y al árbol de expansión.
Paso 4: los nodos adyacentes de 3 se exploran empujándolo hacia la pila y 10 ingresa a la secuencia. Como no hay un nodo adyacente a 10, 3 sale de la pila.
Paso 5: se explora otro nodo adyacente de 3 y se empuja 3 a la pila y se visita 9. No hay ningún nodo adyacente de 9, por lo tanto, 3 sale y se visita el último nodo adyacente de 3, es decir, 2.
Se sigue un proceso similar para todos los nodos hasta que la pila se vacía, lo que indica la condición de detención para el algoritmo transversal. - -> las líneas punteadas en el árbol de expansión se refieren a los bordes posteriores presentes en el gráfico.
De esta manera, todos los nodos en el gráfico son transversales sin repetir ninguno de los nodos.
Ventajas y desventajas
- Ventajas: los requisitos de memoria para este algoritmo son muy inferiores. Menor complejidad de espacio y tiempo que BFS.
- Desventajas: la solución no está garantizada Aplicaciones. Clasificación topológica. Encontrar puentes de grafo.
Ejemplo para implementar el algoritmo DFS
A continuación se muestra el ejemplo para implementar el algoritmo DFS:
Código:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Salida:
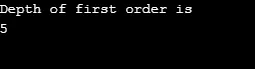
Explicación del programa anterior: Creamos un gráfico con 5 vértices (0, 1, 2, 3, 4) y utilizamos una matriz visitada para realizar un seguimiento de todos los vértices visitados. Luego, para cada nodo cuyos nodos adyacentes existen, el mismo algoritmo se repite hasta que se visiten todos los nodos. Luego, el algoritmo vuelve a llamar al vértice y lo saca de la pila.
Conclusión
El requisito de memoria de este gráfico es menor en comparación con BFS, ya que solo se necesita una pila para mantenerse. Como resultado, se genera un árbol de expansión DFS y una secuencia transversal, pero no es constante. Es posible una secuencia transversal múltiple según el vértice inicial y el vértice de exploración elegido.
Artículos recomendados
Esta es una guía para el algoritmo DFS. Aquí discutimos la explicación paso a paso, recorremos el gráfico en un formato de tabla con ventajas y desventajas. También puede consultar nuestros otros artículos relacionados para obtener más información:
- ¿Qué es HDFS?
- Algoritmos de aprendizaje profundo
- Comandos HDFS
- Algoritmo SHA