Introducción al árbol AVL en la estructura de datos
El árbol AVL en la estructura de datos se refiere a Adelson, Velski y Landis Tree. Esta es una versión mejorada del árbol de búsqueda binario. Tiene todas las características a partir del Árbol de búsqueda binaria, pero solo difiere ya que mantienen una diferencia entre la altura del subárbol izquierdo y el subárbol derecho y también asegura que su valor sea <= 1 en el árbol, esto se conoce como Balance Factor.
Balance Factor = height(left-subtree) − height(right-subtree)
Por ejemplo: considere los siguientes árboles

En el ejemplo anterior, la altura del subárbol derecho = 2 y el izquierdo = 3, por lo tanto BF = 2, que es <= 1, se dice que el árbol está equilibrado.
¿Por qué necesitamos un árbol AVL en DS?
Mientras trabajamos con Binary Search Tree, nos encontramos con un escenario en el que los elementos están ordenados. En tales casos, todos los elementos de la matriz están dispuestos en un lado de la raíz, esto lleva a un aumento en la complejidad temporal de buscar un elemento en una matriz y la complejidad se convierte en O (n), es decir, en la peor de las complejidades del árbol. . Para resolver estos problemas y disminuir el tiempo de búsqueda, los árboles AVL fueron inventados por Adelson, Velski y Landis.
Ejemplo:

En la figura anterior, la altura del subárbol izquierdo = 3 era como
Altura del subárbol derecho = 0
Por lo tanto, Factor de equilibrio = 3-0 = 3. Por lo tanto, buscar un elemento en dicho árbol tiene O (n) de complejidad que es similar a la búsqueda lineal. Para evitar esa búsqueda compleja, se introdujo el árbol AVL donde cada nodo del árbol necesita mantenerse
factor de equilibrio <= 1, de lo contrario se deben realizar varias técnicas de rotación para equilibrar dicho árbol.
Struct AVLNode
(
int data;
struct AVLNode *left, *right;
int ball factor;
);
Tipos de rotaciones
Cuando el factor de equilibrio para el árbol no satisface la condición <= 1, entonces se deben realizar rotaciones en ellos para convertirlo en un árbol equilibrado.
Hay 4 tipos de rotaciones:
1. Rotación izquierda: si la adición de un nodo a la derecha del árbol lo desequilibra, entonces, en ese caso, debe realizarse la rotación izquierda.
2. Rotación a la derecha: si la adición de un nodo a la izquierda del árbol hace que el nodo esté desequilibrado, entonces debe realizarse la rotación a la derecha. En otras palabras, cuando el número de nodos aumenta en el lado izquierdo, surge la necesidad de desplazar los elementos hacia el lado derecho para equilibrarlo, por lo que se dice que es Rotación derecha.
3. Rotación izquierda-derecha: este tipo de rotación es una combinación de las 2 rotaciones explicadas anteriormente. Este tipo de rotación ocurre cuando se agrega un elemento al subárbol derecho de un árbol izquierdo.
En tal caso primero, realice la rotación a la izquierda en el subárbol seguido de una rotación a la derecha del árbol izquierdo.
4. Rotación derecha-izquierda: este tipo de rotación también se compone de una secuencia de más de 2 rotaciones. Este tipo de rotación es necesaria cuando se agrega un elemento a la izquierda del subárbol derecho y el árbol se desequilibra. En tal caso, primero realizamos la rotación derecha en el subárbol derecho y luego la rotación izquierda en el árbol derecho.
Operaciones en el árbol AVL en DS
Debajo de 3 operaciones que se pueden realizar en el árbol AVL: -
1. Buscar
Esta operación es similar a realizar una búsqueda en Binary Search Tree. Los pasos seguidos son los siguientes:
- Lea el elemento proporcionado por el usuario y diga x.
- Compare el elemento desde la raíz, si es el mismo, salga, de lo contrario vaya al siguiente paso.
- Si x
De lo contrario, vaya al niño correcto y compare nuevamente.
Siga los procesos B y C hasta que encuentre el elemento y salga.
Este proceso tiene una complejidad O (log n).
Ejemplo:
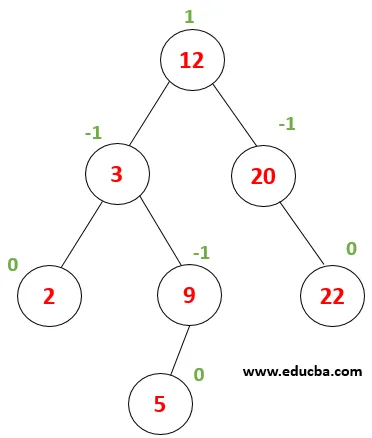 | Considere este árbol, donde debemos realizar una búsqueda del valor de nodo 9. Primero, dejemos que x = 9, valor raíz (12)> x luego, el valor debe estar en el subárbol izquierdo del elemento raíz. |
 | Ahora x se compara con el valor de nodo 3 x> 3, por lo tanto, debemos proceder hacia el subárbol derecho. |
 | Ahora x se compara con el nodo (9), donde 9 == 9 devuelve verdadero. Por lo tanto, la búsqueda de elementos se completa en el árbol. |
2. Inserción
Al insertar un elemento en el árbol AVL, debemos encontrar la ubicación del elemento particular que debe insertarse y luego el elemento se adjunta de la misma manera que una inserción en BST, pero después de eso, se verifica si el árbol aún está equilibrado o no es decir, el factor de equilibrio de un nodo es <= 1. Y se realizan rotaciones particulares según sea necesario.
La complejidad es O (log n).
Ejemplo: considere el siguiente árbol,
 | Cada nodo tiene un factor de equilibrio como 0, -1 o 1, por lo tanto, el árbol está equilibrado. Ahora dejemos lo que sucede cuando se inserta un nodo con valor 1. Se atraviesa el primer árbol para encontrar la ubicación donde debe insertarse … 1 <2, por lo tanto, se escribe como un hijo izquierdo del nodo (2). |
 | Después de la inserción, el nodo (9) se desequilibra con un factor de equilibrio = 2. Ahora se somete a rotación derecha. |
 | Un árbol se equilibra después de la rotación hacia la derecha y, por lo tanto, la operación de inserción se completa con éxito. |
3. Eliminación
Eliminar un elemento en el árbol AVL también comprende buscar un elemento en el árbol y luego eliminarlo. La operación de búsqueda es la misma que BST, y después de encontrar el elemento a eliminar, el elemento se elimina del árbol y los elementos se ajustan para que sea BST nuevamente. Después de comprobar que estos elementos tienen un factor de equilibrio de 0, -1 o 1 y, por lo tanto, se realizan rotaciones adecuadas para equilibrarlo.
Complejidad si O (log n).
 | Considere el árbol dado, cuyos todos tienen un factor de equilibrio de 0, -1 o 1. Ahora eliminemos un nodo con valor 16. Se atraviesa el primer árbol para encontrar el nodo con el valor 16 igual que un algoritmo de búsqueda. |
 | El nodo 16 se reemplazará con el predecesor en orden de este nodo que es el elemento más grande del subárbol izquierdo, es decir, 12 El árbol se ha desequilibrado, por lo tanto, debe realizarse la rotación LL. |
 | Ahora cada nodo se ha equilibrado. |
Conclusión: Árbol AVL en estructura de datos
El árbol AVL es un descendiente del árbol de búsqueda binario, pero supera su inconveniente de complejidad creciente en caso de que los elementos estén ordenados. Supervisa el factor de equilibrio del árbol para que sea 0 o 1 o -1. En caso de que el árbol se desequilibre, se realizan las técnicas de rotación correspondientes para equilibrar el árbol.
Artículos recomendados
Esta es una guía para el árbol AVL en la estructura de datos. Aquí discutimos la Introducción, Operaciones en el árbol AVL en DS y Tipos de rotaciones. También puede consultar nuestros otros artículos relacionados para obtener más información:
- Elementos jQuery
- ¿Qué es la ciencia de datos?
- Tipos de árboles en la estructura de datos
- Tipos de datos de C #