
Fórmula cuartil (tabla de contenido)
- Fórmula
- Ejemplos
Definición de la fórmula del cuartil
Cuartil, como suena su nombre, es un término estadístico que divide los datos en cuartos o cuatro intervalos definidos. Básicamente divide los puntos de datos en un conjunto de datos en 4 trimestres en la recta numérica. Una cosa que debemos tener en cuenta es que los puntos de datos pueden ser aleatorios y tenemos que poner esos números en línea primero en la línea numérica en orden ascendente y luego dividirlos en cuartiles. Básicamente es una versión extendida de la mediana. La mediana divide los datos en dos partes iguales, los cuartiles los dividen en cuatro partes. Una vez que dividimos los datos, los cuatro cuartiles serán:
- El primer cuartil o el cuartil inferior básicamente separan el 25% más bajo de los datos del 75% más alto.
- El segundo cuartil o el cuartil medio también es igual a la mediana, divide los números en 2 partes iguales.
- El tercer cuartil o el cuartil superior separan el 25% más alto de los datos del 75% más bajo.
Fórmula para cuartil:
Digamos que tenemos un conjunto de datos con N puntos de datos:
X - (X1, X2, X3 ……… .. XN)
La fórmula para cuartiles viene dada por:
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
Lo que básicamente significa es que en un conjunto de datos con N puntos de datos:
((N + 1) * 1/4 ) el término es el cuartil inferior
((N + 1) * 2/4 ) el término es el cuartil medio
((N + 1) * 3/4 ) el término es el cuartil superior
El rango intercuartil básicamente las distancias entre el cuartil inferior y el cuartil superior.
Ejemplos de fórmula cuartil (con plantilla de Excel)
Tomemos un ejemplo para comprender el cálculo de Quartile de una mejor manera.
Puede descargar esta plantilla Excel de Quartile Formula aquí - Plantilla Excel de Quartile FormulaFórmula cuartil - Ejemplo # 1
Digamos que tenemos un conjunto de datos A que contiene 19 puntos de datos. Calcule el cuartil para el conjunto de datos A.
Conjunto de datos:
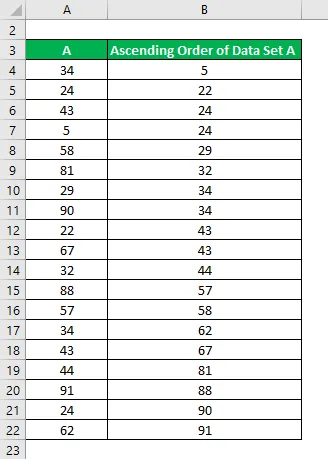
En primer lugar, debe organizar este orden ascendente, es decir, de menor a mayor:
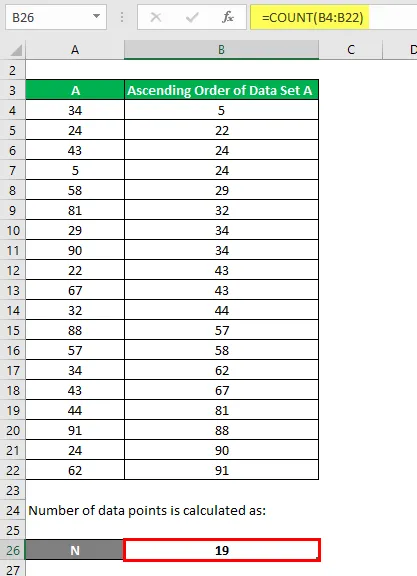
El número de puntos de datos se calcula como:
El cuartil se calcula utilizando la siguiente fórmula dada
Cuartil inferior (Q1) = (N + 1) * 1/4
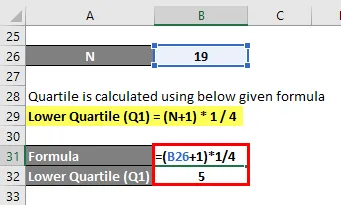
- Cuartil inferior (Q1) = (19 + 1) * 1/4
- Cuartil inferior (Q1) = 20/4 = 5º punto de datos
Cuartil inferior (Q1) = 29
Cuartil medio (Q2) = (N + 1) * 2/4

- Cuartil medio (Q2) = (19 + 1) * 2/4
- Cuartil medio (Q2) = 40/4 = 10º punto de datos
Cuartil Medio (Q2) = 43
Cuartil superior (Q3) = (N + 1) * 3/4

- Cuartil superior (Q3) = (19 + 1) * 3/4
- Cuartil superior (Q3) = 60/4 = 15º punto de datos
Entonces el cuartil superior (Q3) = 67
El rango intercuartil se calcula utilizando la fórmula que se proporciona a continuación
Rango intercuartil = Q3 - Q1
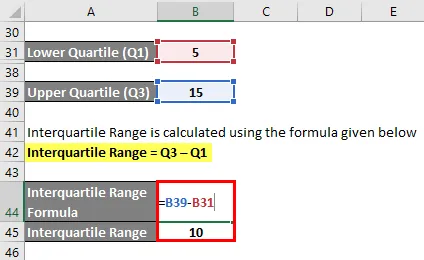
- Rango intercuartil = 15–5
- Rango intercuartil = 10º punto de datos
Entonces rango intercuartil = 43
Si ve el conjunto de datos, la mediana de este conjunto es: (n + 1) / 2 = 20/2 = 10º valor, es decir 43, esto es lo mismo que Q2.
Inferencia:
- El valor 29 divide el conjunto de datos de tal manera que el 25% más bajo está por encima de él y el 75% más alto está por debajo de él
- El valor 43 divide el conjunto de datos en dos partes iguales
- El valor 67 divide el conjunto de datos de tal manera que el 25% más alto está por debajo de él y el 75% más bajo está por encima de él
Fórmula cuartil - Ejemplo # 2
Veamos otro ejemplo de cómo las empresas y los negocios pueden usar esta herramienta para tomar una decisión informada sobre qué producto producir.
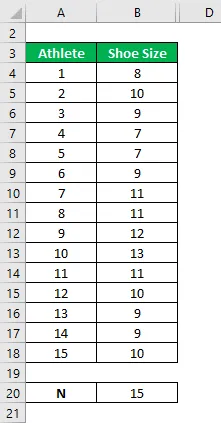
Supongamos que usted es un fabricante de zapatos para correr y una marca conocida entre los atletas que corren un maratón, practican deportes, etc. Ha reunido los datos de los tamaños de calzado que usan estos atletas para que en el futuro produzca más de ese tamaño. para satisfacer la demanda
Has recogido una muestra de 15 atletas de diferentes deportes. Calcula el cuartil.
El conjunto de datos se proporciona a continuación:
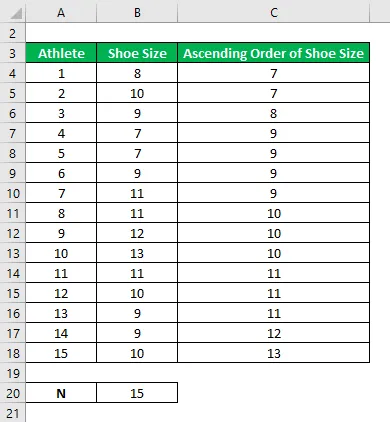
Organice el tamaño del zapato en orden ascendente.
El cuartil se calcula utilizando la siguiente fórmula dada
Cuartil inferior (Q1) = (N + 1) * 1/4
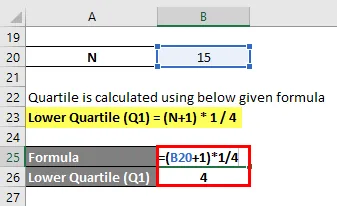
- Cuartil inferior (Q1) = (15 + 1) * 1/4
- Cuartil inferior (Q1) = 16/4 = 4º punto de datos
Cuartil inferior (Q1) = 10
Cuartil medio (Q2) = (N + 1) * 2/4
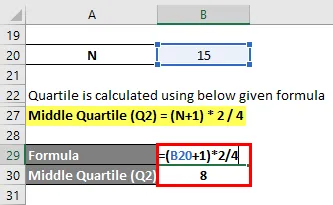
- Cuartil medio (Q2) = (15 + 1) * 2/4
- Cuartil medio (Q2) = 32/4 = 8º punto de datos
Cuartil medio (Q2) = 10
Cuartil superior (Q3) = (N + 1) * 3/4

- Cuartil superior (Q3) = (15 + 1) * 3/4
- Cuartil superior (Q3) = 48/4 = 12º punto de datos
Entonces el cuartil superior (Q3) = 11
El rango intercuartil se calcula utilizando la fórmula que se proporciona a continuación
Rango intercuartil = Q3 - Q1
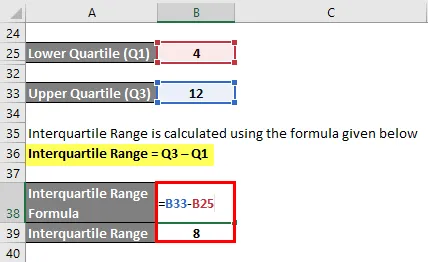
- Rango intercuartil = 12 - 4
- Rango intercuartil = 8º punto de datos
Entonces rango intercuartil = 10
Explicación
Para comprender mejor los cuartiles, necesitamos entender la mediana de una mejor manera. La mediana divide el conjunto de datos en exactamente dos mitades iguales, pero no nos dice nada acerca de la difusión de los datos en ambos lados. Un cuartil es una versión extendida de eso y al dividir el conjunto de datos en cuatro partes, se ocupa de la distribución de valores por encima y por debajo de la media. Además, existen otras herramientas estadísticas que nos informan sobre el rango del conjunto de datos, el centro del conjunto de datos, etc. Pero la fórmula del cuartil nos ayuda a comprender todos estos elementos. La mediana, que es el cuartil medio, nos dice el punto central y los cuartiles superior e inferior nos dicen la extensión.
Relevancia y usos de la fórmula del cuartil
Como se discutió anteriormente, la fórmula del cuartil nos ayuda a dividir los datos en cuatro partes muy rápidamente y eventualmente nos facilita la comprensión de los datos en estas partes. Por ejemplo, un maestro de clase quiere premiar al 25% superior de los estudiantes con golosinas y regalos y quiere dar otra oportunidad al 25% inferior de los estudiantes para mejorar su puntaje. Puede usar cuartiles y puede dividir los datos. Entonces, si los cuartiles se dicen 51, 65, 72 y el puntaje de un estudiante es de 78, obtendrá golosinas. Si otro estudiante tiene un puntaje de 48, tendrá otra oportunidad de mejorar el puntaje, una interpretación rápida y fácil.
Artículos recomendados
Esta ha sido una guía para la fórmula del cuartil. Aquí discutimos la definición y cómo calcular Quartile junto con ejemplos prácticos y una plantilla de Excel descargable. También puede consultar los siguientes artículos para obtener más información:
- Ejemplos de fórmula de valores atípicos (plantilla de Excel)
- Calculadora para fórmula de rango de percentil
- Fórmula para calcular R cuadrado ajustado
- ¿Cómo calcular la distribución binomial?
- Fórmula de desviación del cuartil | Ejemplos | Calculadora