Introducción al algoritmo de agrupamiento jerárquico
El algoritmo de agrupamiento jerárquico es una técnica de aprendizaje automático no supervisada. Su objetivo es encontrar agrupaciones naturales basadas en las características de los datos.
El algoritmo de agrupamiento jerárquico tiene como objetivo encontrar grupos anidados de los datos mediante la construcción de la jerarquía. Es similar a la taxonomía biológica del reino vegetal o animal. Los grupos jerárquicos generalmente se representan utilizando el árbol jerárquico conocido como dendrograma.
Tipos de algoritmo de agrupamiento jerárquico
Los algoritmos de agrupamiento jerárquico son de 2 tipos:
- Divisivo
- Aglomerativo
1. Divisivo
Este es un enfoque de arriba hacia abajo, donde inicialmente considera todos los datos como un grupo, y luego divide los datos de manera iterativa en subgrupos. Si se conoce el número de un algoritmo de agrupamiento jerárquico, entonces el proceso de división se detiene una vez que se alcanza el número de grupos. De lo contrario, el proceso se detiene cuando los datos ya no se pueden dividir, lo que significa que el subgrupo obtenido de la iteración actual es el mismo que el obtenido de la iteración anterior (también se puede considerar que la división se detiene cuando cada punto de datos es un clúster )
2. Aglomerativo
Es un enfoque ascendente que se basa en la fusión de clústeres. Inicialmente, los datos se dividen en grupos de m singleton (donde el valor de m es el número de muestras / puntos de datos). Dos grupos se fusionan en uno de forma iterativa, lo que reduce el número de grupos en cada iteración. Este proceso de fusión de grupos se detiene cuando todos los grupos se han fusionado en uno o se alcanza el número de grupos deseados.
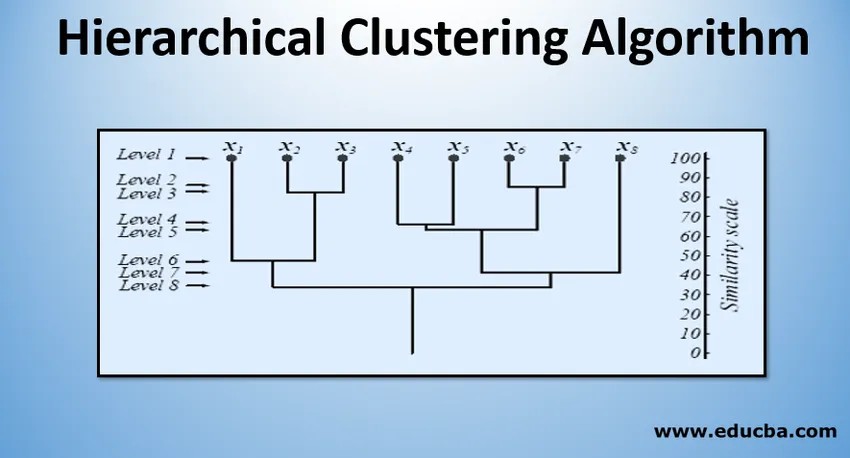
En el nivel 1, hay m clústeres que se reducen a 1 clúster en el nivel m. Los puntos de datos que se fusionan para formar un grupo en un nivel inferior también permanecen en el mismo grupo en los niveles superiores. Por ejemplo, suponga que hay 8 puntos x1..x8, por lo que inicialmente hay 8 grupos en el nivel 1. Suponga que los puntos x1 y x2 se fusionan en un grupo en el nivel 2, luego, hasta el nivel 8, permanecen en el mismo grupo.
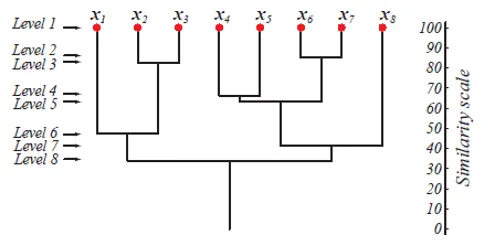
La figura anterior muestra una representación de dendrograma del enfoque de agrupación de aglomeración para 8 puntos de datos, así como la escala de similitud correspondiente a cada nivel.
Los niveles de los grupos nos dan una idea de cuán similares son los puntos de datos en los grupos. Como se muestra en la figura 1, antes los puntos de datos se fusionan en un clúster, son similares. Por lo tanto, los puntos de datos dentro de un grupo en el nivel 2 (por ejemplo, x2 y x3) son más similares que los puntos de datos en un grupo en el nivel 6 (por ejemplo, x1 y x2).
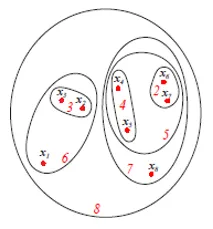
La figura anterior muestra la representación del diagrama de Set o Venn del enfoque de agrupamiento aglomerativo de los 8 puntos de datos mencionados anteriormente. Tanto los dendrogramas como las representaciones de conjuntos se pueden usar para la agrupación. Sin embargo, un dendrograma suele ser preferible. La representación de activos no puede representar cuantitativamente las similitudes del clúster.
Pasos para el algoritmo de agrupamiento jerárquico
Sigamos los siguientes pasos para el algoritmo de agrupamiento jerárquico que se dan a continuación:
1. Algoritmo
Algoritmo de agrupamiento jerárquico aglomerativo
- Comience a inicializar c, c1 = n, Di = (xi), i = 1, …, n '
- Do c1 = c1 - 1
- Encuentra los grupos más cercanos, por ejemplo, Di y Dj
- Fusionar Di y Dj
- Hasta que c = c1
- Regresar c agrupaciones
- Final
Este algoritmo comienza con n grupos inicialmente donde cada punto de datos es un grupo. Con cada iteración, el número de grupos se reduce en 1 a medida que se fusionan los 2 grupos más cercanos. Este proceso continúa hasta que el número de clústeres se reduce al valor predefinido c.
¿Cómo decidir qué grupos están cerca?
Eso se define usando varias métricas de distancia que son las siguientes:
- La distancia mínima entre los grupos dmin (Di, Dj). Útil para solteros.
- La distancia máxima entre los grupos dmax (Di, Dj). Útil para completar.
- La distancia media entre los grupos davg (Di, Dj).
¿Qué es el enlace único y el enlace completo?
- Cuando se usa dmin (di, dj) para encontrar la distancia entre dos grupos, y el algoritmo termina si la distancia entre los grupos más cercanos excede un umbral, entonces el algoritmo se llama algoritmo de enlace único.
- Cuando se usa dmax (Di, Dj) para encontrar la distancia entre dos grupos, y el algoritmo termina si la distancia entre los grupos más cercanos excede un umbral, entonces el algoritmo se llama algoritmo de enlace completo.
- Consideremos cada punto de datos como un nodo de un gráfico. Hay una ventaja entre dos puntos de datos si pertenecen al mismo clúster. Cuando se fusionan dos grupos más cercanos, se agrega un borde. Se llama un enlace único porque existe una ruta única de un nodo a otro.
- El algoritmo de enlace completo combina dos grupos al minimizar la distancia entre los dos puntos más lejanos.
- Un algoritmo de enlace único genera un árbol de expansión. Sin embargo, este algoritmo es susceptible al ruido. Un algoritmo de enlace completo genera un gráfico completo.
¿Cuál es la complejidad temporal del algoritmo?
Supongamos que tenemos n patrones en el espacio d-dimensional, y usamos dmin (Di, Dj) para formar c grupos. Necesitamos calcular n (n - 1) distancias entre puntos, cada una de las cuales es un cálculo de O (d 2 ), y colocar los resultados en una tabla de distancias entre puntos. La complejidad del espacio es O (n 2 ). Encontrar el par de distancia mínima (para la primera fusión) requiere que recorramos la lista completa, manteniendo el índice de la distancia más pequeña.
Así, para el primer paso aglomerativo, la complejidad es O (n (n - 1) (d 2 + 1)) = O (n 2 d 2 ). Para otro paso de aglomeración arbitrario (es decir, de c1 a c1 - 1), simplemente pasamos por las distancias "no utilizadas" n (n - 1) - c1 en la lista y encontramos la más pequeña para la cual x y x 'se encuentran en diferentes grupos . Esto es, nuevamente, O (n (n − 1) −c1). La complejidad del tiempo total es, por lo tanto, O (cn 2 d 2 ), y en condiciones típicas n >> c.
2. Visualización
Una vez que los datos se dividen en grupos, es una buena práctica visualizar los grupos para tener una idea de cómo se ve la agrupación. Pero visualizar estos datos de alta dimensión es difícil. Por lo tanto, utilizamos el análisis de componentes principales (PCA) para la visualización. Después de PCA, obtenemos los puntos de datos en el espacio de baja dimensión (generalmente 2D o 3D) que podemos trazar para ver la agrupación.
Nota: La dimensión alta significa una gran cantidad de características y no una cantidad de puntos de datos.3. Evaluación
Uno de los métodos para la evaluación de grupos es que la distancia de los puntos entre los grupos (distancia entre grupos) debe ser mucho mayor que la distancia de los puntos dentro del grupo (distancia dentro del grupo).
Conclusión
Los siguientes son algunos puntos clave:
- El algoritmo de agrupamiento jerárquico se usa para encontrar patrones anidados en datos
- La agrupación jerárquica es de 2 tipos: divisiva y aglomerativa
- El dendrograma y el diagrama de set / Venn se pueden usar para la representación
- El enlace único combina dos grupos al minimizar la distancia mínima entre ellos. Se forma una extensión
- La vinculación completa combina dos grupos al minimizar la distancia máxima entre Se forma un gráfico completo.
- La complejidad temporal total del algoritmo de agrupamiento jerárquico es O (cn 2 d 2 ), donde c es el número predefinido de grupos, n es el número de patrones yd es el espacio d-dimensional de los n patrones.
Artículos recomendados
Esta es una guía del algoritmo de agrupación jerárquica. Aquí discutimos los tipos y pasos de los algoritmos de agrupamiento jerárquico. También puede consultar los siguientes artículos para obtener más información.
- Análisis de agrupamiento jerárquico
- Agrupación jerárquica en R '
- Algoritmo de agrupamiento
- ¿Qué es el agrupamiento en minería de datos?
- Agrupación jerárquica | Agrupamiento Aglomerativo y Divisivo
- Algoritmo de C ++ | Ejemplos de algoritmo C ++