Introducción a la agrupación jerárquica
- Recientemente, uno de nuestros clientes le pidió a nuestro equipo que presentara una lista de segmentos con un orden de importancia dentro de sus clientes para dirigirlos a franquiciar uno de sus productos recién lanzados. Claramente, solo segmentar a los clientes usando el agrupamiento parcial (k-means, c-fuzzy) no resaltará el orden de importancia que es donde el agrupamiento jerárquico entra en escena.
- La agrupación jerárquica es separar los datos en diferentes grupos en función de algunas medidas de similitud conocidas como agrupaciones, que se dirigen esencialmente a la construcción de la jerarquía entre agrupaciones. Básicamente es un aprendizaje no supervisado y la elección de los atributos para medir la similitud es específica de la aplicación.
El grupo de jerarquía de datos
- Agrupamiento Aglomerativo
- Agrupación divisiva
Tomemos un ejemplo de datos, calificaciones obtenidas por 5 estudiantes para agruparlos en una próxima competencia.
| Estudiante | Marcas |
| UN | 10 |
| si | 7 7 |
| C | 28 |
| re | 20 |
| mi | 35s |
1. Agrupación aglomerativa
- Para comenzar, consideramos cada punto / elemento individual aquí ponderar como grupos y seguimos fusionando los puntos / elementos similares para formar un nuevo grupo en el nuevo nivel hasta que nos quedemos con el grupo único es un enfoque de abajo hacia arriba.
- El enlace único y el enlace completo son dos ejemplos populares de agrupamiento aglomerativo. Aparte de eso Enlace promedio y enlace Centroide. En un enlace único, fusionamos en cada paso los dos grupos, cuyos dos miembros más cercanos tienen la menor distancia. En un enlace completo, nos fusionamos en los miembros de la distancia más pequeña que proporcionan la distancia máxima por pares más pequeña.
- Matriz de proximidad, es el núcleo para realizar la agrupación jerárquica, que proporciona la distancia entre cada uno de los puntos.
- Hagamos una matriz de proximidad para nuestros datos dados en la tabla, ya que estamos calculando la distancia entre cada uno de los puntos con otros puntos, será una matriz asimétrica de forma n × n, en nuestro caso matrices de 5 × 5.
Un método popular para los cálculos de distancia son:
- Distancia euclidiana (cuadrada)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Distancia de Manhattan
dist((x, y), (a, b)) =|x−c|+|y−d|
La distancia euclidiana se usa más comúnmente, usaremos la misma aquí, e iremos con enlaces complejos.
| Estudiante (grupos) | UN | si | C | re | mi |
| UN | 0 0 | 3 | 18 años | 10 | 25 |
| si | 3 | 0 0 | 21 | 13 | 28 |
| C | 18 años | 21 | 0 0 | 8 | 7 7 |
| re | 10 | 13 | 8 | 0 0 | 15 |
| mi | 25 | 28 | 7 7 | 15 | 0 0 |
Los elementos diagonales de la matriz de proximidad siempre serán 0, ya que la distancia entre el punto con el mismo punto siempre será 0, por lo tanto, los elementos diagonales están exentos de consideración para la agrupación.
Aquí, en la iteración 1, la distancia más pequeña es 3, por lo tanto, fusionamos A y B para formar un grupo, nuevamente formamos una nueva matriz de proximidad con el grupo (A, B) tomando el punto de grupo (A, B) como 10, es decir, un máximo de ( 7, 10) entonces la matriz de proximidad recién formada sería
| Racimos | (A, B) | C | re | mi |
| (A, B) | 0 0 | 18 años | 10 | 25 |
| C | 18 años | 0 0 | 8 | 7 7 |
| re | 10 | 8 | 0 0 | 15 |
| mi | 25 | 7 7 | 15 | 0 0 |
En la iteración 2, 7 es la distancia mínima, por lo tanto, fusionamos C y E formando un nuevo grupo (C, E), repetimos el proceso seguido en la iteración 1 hasta que terminemos con el grupo único, aquí nos detenemos en la iteración 4.
Todo el proceso se representa en la siguiente figura:
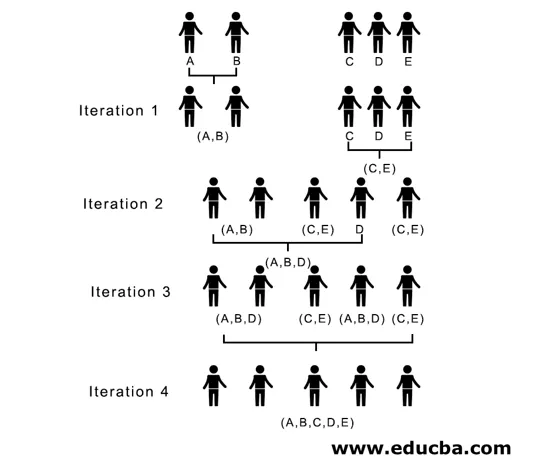
(A, B, D) y (D, E) son los 2 grupos formados en la iteración 3, en la última iteración podemos ver que nos queda un solo grupo.
2. Agrupación divisiva
Para comenzar, consideramos todos los puntos como un solo grupo y los separamos por la mayor distancia hasta que terminemos con puntos individuales como grupos individuales (no necesariamente podemos detenernos en el medio, depende del número mínimo de elementos que queremos en cada grupo) en cada paso Es todo lo contrario de la agrupación aglomerativa y es un enfoque de arriba hacia abajo. La agrupación divisiva es una forma repetitiva de k significa agrupación.
Elegir entre Agrupamiento Aglomerativo y Divisivo depende nuevamente de la aplicación, aunque pocos puntos a considerar son:
- Divisivo es más complejo que el agrupamiento aglomerativo.
- La agrupación divisiva es más eficiente si no generamos una jerarquía completa hasta los puntos de datos individuales.
- La agrupación aglomerativa toma una decisión al considerar los patrones locales, sin tener en cuenta los patrones globales que inicialmente no pueden revertirse.
Visualización de agrupamiento jerárquico
Un método súper útil para visualizar la agrupación jerárquica que ayuda en los negocios es Dendogram. Los dendogramas son estructuras en forma de árbol que registran la secuencia de fusiones y divisiones en las que la línea vertical representa la distancia entre los grupos, la distancia entre las líneas verticales y la distancia entre los grupos es directamente proporcional, es decir, a mayor distancia es probable que los grupos sean diferentes.
Podemos usar el dendograma para decidir el número de grupos, simplemente dibuje una línea que se cruce con una línea vertical más larga en el dendograma, un número de líneas verticales intersectadas será el número de grupos a considerar.
A continuación se muestra el ejemplo de Dendogram.
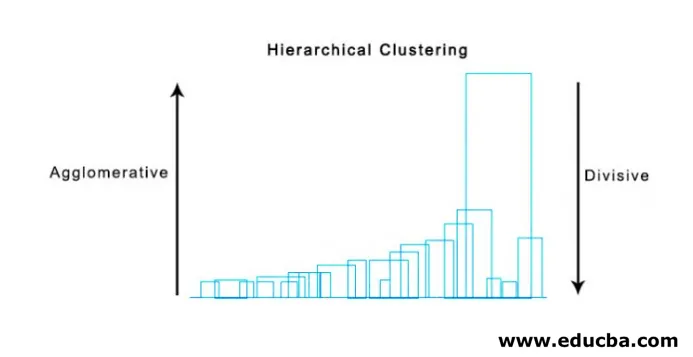
Hay paquetes de Python bastante simples y directos y sus funciones para realizar agrupamientos jerárquicos y dendogramas de trazado.
- La jerarquía de scipy.
- Cluster.hierarchy.dendogram para visualización.
Escenarios comunes en los que se utiliza la agrupación jerárquica
- Segmentación de clientes para la comercialización de productos o servicios.
- Ciudad planeando identificar los lugares para construir estructuras / servicios / construcción.
- Análisis de redes sociales, por ejemplo, identifique a todos los fanáticos de MS Dhoni para anunciar su película biográfica.
Ventajas de la agrupación jerárquica
Las ventajas se dan a continuación:
- En el caso de la agrupación parcial como k-means, el número de agrupaciones debe conocerse antes de la agrupación, lo que no es posible en aplicaciones prácticas, mientras que en la agrupación jerárquica no se requiere conocimiento previo de la cantidad de agrupaciones.
- La agrupación jerárquica genera una jerarquía, es decir, una estructura más informativa que el conjunto no estructurado de agrupaciones planas devueltas por agrupación parcial.
- La agrupación jerárquica es fácil de implementar.
- Presenta resultados en la mayoría de los escenarios.
Conclusión
El tipo de agrupación marca la gran diferencia cuando se presentan los datos, la agrupación jerárquica, que es más informativa y fácil de analizar, es más preferible que la agrupación parcial. Y a menudo se asocia con mapas de calor. Sin olvidar que los atributos elegidos para calcular la similitud o la disimilitud influyen predominantemente tanto en los grupos como en la jerarquía.
Artículos recomendados
Esta es una guía para la agrupación jerárquica. Aquí discutimos la introducción, las ventajas de la agrupación jerárquica y los escenarios comunes en los que se utiliza la agrupación jerárquica. También puede consultar nuestros otros artículos sugeridos para obtener más información:
- Algoritmo de agrupamiento
- Agrupación en Machine Learning
- Agrupación jerárquica en R
- Métodos de agrupamiento
- ¿Cómo eliminar la jerarquía en Tableau?