
Introducción a los ejemplos de desviación estándar
Hay muchos ejemplos de desviaciones estándar. La desviación estándar es la medida de la dispersión del conjunto de datos, es decir, qué tan dispersos están los números. Es útil para comparar los diferentes conjuntos de datos que pueden tener la misma media pero el rango diferente. El siguiente ejemplo de desviación estándar diferente proporciona una comprensión sobre el tipo más común de situaciones en las que se calcula la desviación estándar y cómo se puede calcular la misma
Ejemplos de desviación estándar
A continuación se muestran los ejemplos de la desviación estándar
Desviación Estándar - Ejemplo # 1
Las acciones de la Compañía Z se venden a $ 50 por acción y las mismas ofertas después de los pagos del próximo año:
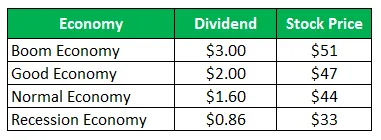
Calcule la desviación estándar cuando los cuatro escenarios se dan son igualmente probables.
Solución:
Los cálculos del rendimiento del período de mantenimiento (HPR) son los siguientes:
Fórmula de HPR
HPR = ((Valor de fin de período - Valor original) + Ingresos) / Valor original) * 100
Para la economía de auge
- HPR (Auge) = ((51-50) + 3) / 50 = 8.00%
- HPR (Bueno) = ((47-50) + 2) / 50 = -2.00%
- HPR (Normal) = ((44-50) + 1.60) / 50 = -8.80%
- HPR (recesión) = ((33-50) + 0.86) / 50 = -32.28%
Cálculo del rendimiento esperado
Como todos los escenarios son igualmente probables, la probabilidad de todos será de ¼
Fórmula de retorno esperado
Retorno esperado = (Probabilidad de auge * Retorno de auge) + (Probabilidad de bien * Retorno de bueno) + (Probabilidad de normal * Retorno de normal) + (Probabilidad de recesión * Retorno de recesión)
- Retorno esperado = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8.80%) + (1/4 x -32.28%)
- Retorno esperado = -8.77%
Cálculo de desviación estándar
Fórmula de varianza
Varianza = (Probabilidad de auge * (Retorno de auge - Retorno total esperado) 2) + (Probabilidad de bien * (Retorno de bueno - Retorno total esperado) 2) + (Probabilidad de normal * (Retorno de normal - Retorno total esperado) 2 ) + (Probabilidad de recesión * (Retorno de la recesión - Retorno total esperado) 2)
- Varianza = 1/4 (8 - (-8.77)) 2 + 1/4 (-2 - (-8.77)) 2 + 1/4 (-8.80 - (-8.77)) 2 + 1/4 (-32.28 - (-8.77)) 2
- Varianza = 219.95
Fórmula de desviación estándar
La desviación estándar será la raíz cuadrada de la varianza
Desviación estándar = √Variancia
- Desviación estándar = √ 219.95
- Desviación estándar = 14.83%
Ejemplo de desviación estándar - 2
Desviación estándar en el caso de dos empresas en cartera
Las acciones ordinarias de la Compañía A se venden a $ 28 por acción y las mismas ofertas después de los pagos del próximo año.

Las acciones comunes de la Compañía B se venden a $ 93 por acción y las mismas ofertas después de los pagos para el próximo año:

(a) Calcule la desviación estándar de la Compañía A
(b) Calcule la desviación estándar de la Compañía B
(c) Calcule la desviación estándar de la cartera si la mitad de la inversión se realiza en la Compañía A y el resto en la Compañía B
Solución:
Para la empresa A
Cálculos de retorno del período de mantenimiento (HPR)
Fórmula de HPR
HPR = ((Valor de fin de período - Valor original) + Ingresos) / Valor original) * 100
- HPR (auge) = ((20-28) + 1) / 28 = -25.00%
- HPR (Normal) = ((30-28) + 1.50 / 28 = 12.50%
- HPR (recesión) = ((38-28) + 5) / 28 = 53.57%
Cálculo del rendimiento esperado de la empresa A
Fórmula de retorno esperado
Retorno esperado = (Probabilidad de auge * Retorno de auge) + (Probabilidad de normal * Retorno de normal) + (Probabilidad de recesión * Retorno de recesión)
- Retorno esperado = (0.45 x -25.00%) + (0.35 x 12.50%) + (0.20 x 53.57%)
- Retorno esperado = 3.84%
Cálculo de la desviación estándar de la empresa A
Fórmula de varianza
Varianza = (Probabilidad de auge * (Retorno de auge - Retorno total esperado) 2) + (Probabilidad de normalidad * (Retorno de normal - Retorno total esperado) 2 ) + (Probabilidad de recesión * (Retorno de recesión - Retorno total esperado) 2)
- Varianza = 0.45 (-25.00 - (3.84)) 2 + 0.35 (12.50 - (3.84)) 2 + 0.20 (53.57 - (3.84)) 2
- Varianza = 895.15
Fórmula de desviación estándar
La desviación estándar será la raíz cuadrada de la varianza
Desviación estándar = √Variancia
- Desviación estándar = √ 895.15
- Desviación estándar = 29.92%
Para la empresa B
Cálculos de retorno del período de mantenimiento (HPR)
Fórmula de HPR
HPR = ((Valor de fin de período - Valor original) + Ingresos) / Valor original) * 100
HPR (Auge) = ((200-93) +7) / 93 = 122.58%
HPR (Normal) = ((105-93) + 5.50 / 93 = 18.82%
HPR (recesión) = ((4-93) +2) / 93 = -93.55%
Cálculo del rendimiento esperado
Fórmula de retorno esperado
Retorno esperado = (Probabilidad de auge * Retorno de auge) + (Probabilidad de normal * Retorno de normal) + (Probabilidad de recesión * Retorno de recesión)
- Retorno esperado = (0.45x 122.58%) + (0.35 x 18.82%) + (0.20 x -93.55%)
- Retorno esperado = 43.04%
Cálculo de desviación estándar
Fórmula de varianza
Varianza = (Probabilidad de auge * (Retorno de auge - Retorno total esperado) 2) + (Probabilidad de normalidad * (Retorno de normal - Retorno total esperado) 2 ) + (Probabilidad de recesión * (Retorno de recesión - Retorno total esperado) 2)
- Varianza = 0.45 (122.58– (43.04)) 2 + 0.35 (18.82– (43.04)) 2 + 0.20 (-93.55– (43.04)) 2
- Varianza = 6783.65
Fórmula de desviación estándar
La desviación estándar será la raíz cuadrada de la varianza
Desviación estándar = √Variancia
- Desviación estándar = √6783.65
- Desviación Estándar = 82.36%
Cálculo del rendimiento esperado y la desviación estándar de una cartera mitad invertida en la empresa A y mitad en la empresa B.
Desviación Estándar de la Compañía A = 29.92%
Desviación Estándar de la Compañía B = 82.36%
Peso de la empresa A = 0.50
Peso de la empresa B = 0.50
La fórmula de la desviación estándar de la cartera
Desviación estándar de la cartera = (peso de la empresa A * rendimiento esperado de la empresa A) + ((peso de la empresa B * rendimiento esperado de la empresa B)
- Desviación estándar de cartera = (0.50 * 29.92) + (0.50 * 82.36)
- Desviación estándar de cartera = 56.14%
Análisis
La desviación estándar de la cartera es menor que la de cualquiera de las acciones porque las acciones están diversificadas en diferentes acciones. La diversificación conduce a una reducción en el riesgo a menos que exista una correlación perfecta entre los rendimientos de las inversiones de cartera.
Conclusión: ejemplos de desviación estándar
La desviación estándar mide la dispersión del conjunto de datos que es relativa a su media. Se calcula como la raíz cuadrada de la varianza. Cuanto mayor sea la desviación estándar de la seguridad, mayor será la variación entre cada uno de los precios y la media, lo que muestra que el rango de precios es grande. Los ejemplos mencionados anteriormente son algunos de los ejemplos de desviación estándar de diferentes maneras. También hay varios otros ejemplos que muestran que la desviación estándar se puede calcular utilizando otros datos.
Artículos recomendados
Esta ha sido una guía para los ejemplos de desviación estándar. Aquí discutimos los diversos ejemplos de desviación estándar junto con una explicación detallada . También puede echar un vistazo a los siguientes artículos para obtener más información:
- Ejemplo de costos fijos
- Ejemplo de costeo variable
- Ejemplo de investigación cuantitativa
- Ejemplos de competencia monopolística