
Fórmula de desviación del cuartil (tabla de contenido)
- Fórmula
- Ejemplos
- Calculadora
¿Qué es la fórmula de desviación del cuartil?
La desviación del cuartil (QD) es el producto de la mitad de la diferencia entre los cuartiles superior e inferior. Matemáticamente podemos definir como:
Quartile Deviation = (Q 3 – Q 1 ) / 2
La desviación del cuartil define la medida absoluta de dispersión. Mientras que la medida relativa correspondiente a QD, se conoce como el coeficiente de QD, que se obtiene aplicando el cierto conjunto de la fórmula:
Coefficient of Quartile Deviation = (Q 3 – Q 1 ) / (Q 3 + Q 1 )
Se utiliza un coeficiente de QD para estudiar y comparar el grado de variación en diferentes situaciones.
Ejemplos de fórmula de desviación del cuartil (con plantilla de Excel)
Tomemos un ejemplo para comprender el cálculo de la fórmula de desviación del cuartil de una mejor manera.
Puede descargar esta plantilla Excel de la fórmula de desviación del cuartil aquí - Plantilla Excel de la fórmula de la desviación del cuartilFórmula de desviación del cuartil - Ejemplo # 1
El número de quejas presentadas contra el robo de los vehículos en un día se calculó para los próximos 10 días. Y los datos se dan a continuación. Calcule la desviación del cuartil y su coeficiente para el caso de distribución discreta dado.
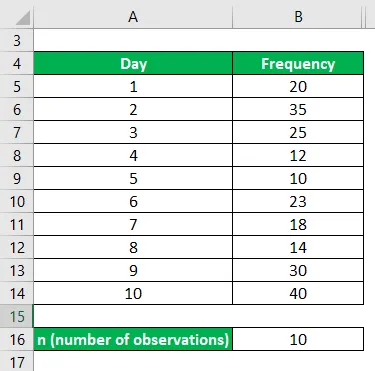
Solución:
Organizar los datos en orden ascendente
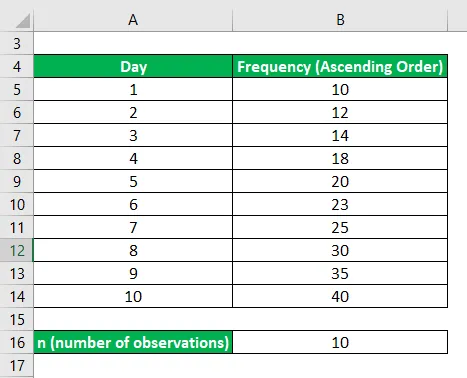
Ahora, encontraremos el primer cuartil, la forma en que se encuentra a medio camino entre el valor más bajo y la mediana; donde el tercer cuartil se encuentra a medio camino entre la mediana y el valor más grande.
El primer cuartil (Q 1 ) se calcula utilizando la fórmula que se proporciona a continuación
Primer cuartil (Q 1 )
Q i = (i * (n + 1) / 4) th observación
Q 1 = (1 * (10 + 1) / 4) th observación
Q 1 = (1 * (10 + 1) / 4) th observación
Q 1 = 2.75 observacion
Entonces, la observación 2.75 se encuentra entre el segundo y tercer valor en el grupo ordenado, o en el medio entre 12 y 14, por lo tanto
El primer cuartil (Q 1 ) se calcula como
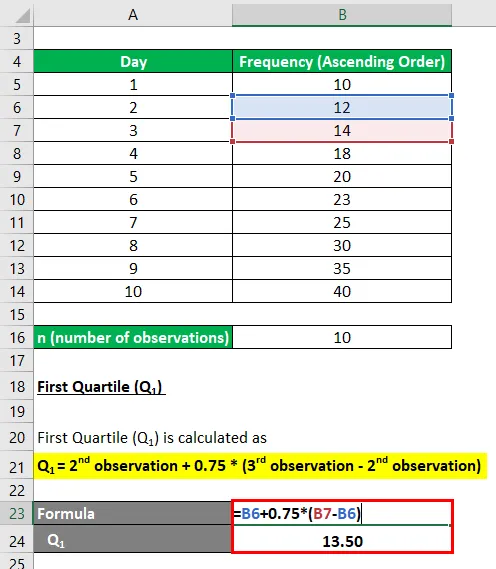
- Q 1 = 2 a observación + 0, 75 * (3 a observación - 2 a observación)
- Q 1 = 12 + 0.75 * (14-12)
- Q 1 = 12 + 1.50
- Q 1 = 13.50
El tercer cuartil (Q 3 ) se calcula utilizando la fórmula que se proporciona a continuación
Tercer cuartil (Q 3 )
Q i = (i * (n + 1) / 4) th obsevation
- Q 3 = (1 * (n + 1) / 4) th obsevation
- Q 3 = ((10 + 1) / 4) th obsevation
- Q 3 = 8.25 a observación
Entonces, la observación 8..25 se encuentra entre los valores 8 y 9 en el grupo ordenado, o entre 30 y 35, por lo tanto
El tercer cuartil (Q 3 ) se calcula como
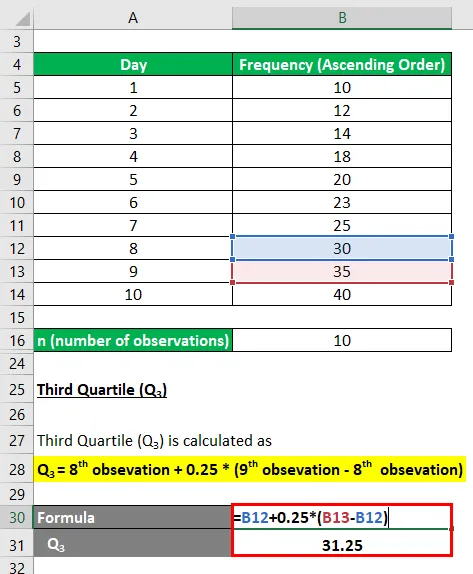
- Q 3 = octava obsevación + 0.25 * (novena obsevación - octava obsevación)
- Q 3 = 30 + 0.25 * (35-30)
- Q 3 = 31.25
Ahora, usando los valores del cuartil Q1 y Q3, calcularemos su desviación del cuartil y su coeficiente de la siguiente manera:
La desviación del cuartil se calcula utilizando la fórmula que se proporciona a continuación.
Desviación del cuartil = (Q 3 - Q 1 ) / 2
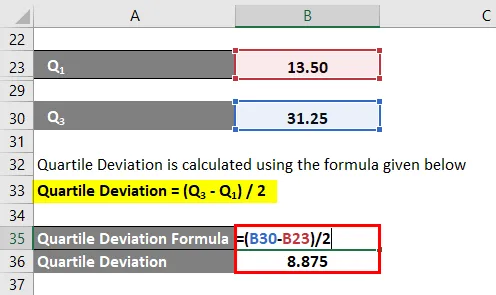
- Desviación del cuartil = (31.25 - 13.50) / 2
- Desviación del cuartil = 8.875
El coeficiente de desviación del cuartil se calcula utilizando la fórmula que se proporciona a continuación
Coeficiente de desviación del cuartil = (Q 3 - Q 1 ) / (Q 3 + Q 1 )
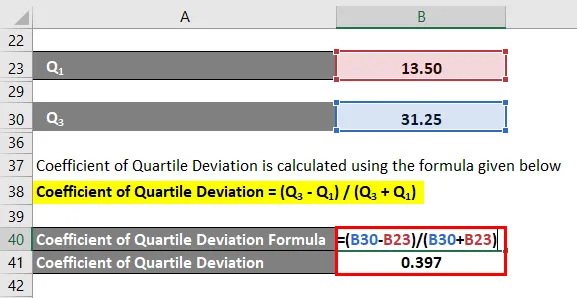
- Coeficiente de desviación del cuartil = (31.25 - 13.50) /(31.25 + 13.50)
- Coeficiente de desviación del cuartil = 0. 397
Fórmula de desviación del cuartil - Ejemplo # 2
Las siguientes son las observaciones que muestran las ventas de un día de un centro comercial, donde determinamos la frecuencia de los primeros 50 clientes de diferentes grupos de edad. Ahora, necesitamos calcular la desviación del cuartil y el coeficiente de la desviación del cuartil.

Solución:
En el caso de la distribución de frecuencia, los cuartiles se pueden calcular utilizando la fórmula:
Q i = l + (h / f) * (i * (N / 4) - c) ; i = 1, 2, 3
Dónde,
- l = límite inferior del grupo cuartil
- h = Ancho del grupo cuartil
- f = Frecuencia del grupo cuartil
- N = Número total de observaciones
- c = frecuencia acumulativa
Primero, tenemos que calcular la tabla de frecuencia acumulativa
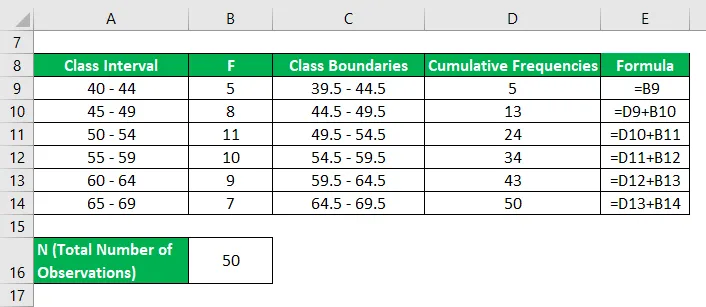
El primer cuartil (Q 1 ) se calcula utilizando la fórmula que se proporciona a continuación
Primer cuartil (Q 1 )
Q i = (i * (N) / 4) th obsevation
- Q 1 = (1 * (50) / 4) th obsevation
- Q 1 = 12.50 a obsevación
Dado que el valor 12.50 está en el intervalo 44.5 - 49.5
Por lo tanto, el Grupo de Q1 es (44.5 - 49.5)
Q i = l + (h / f) * (i * (N / 4) - c)
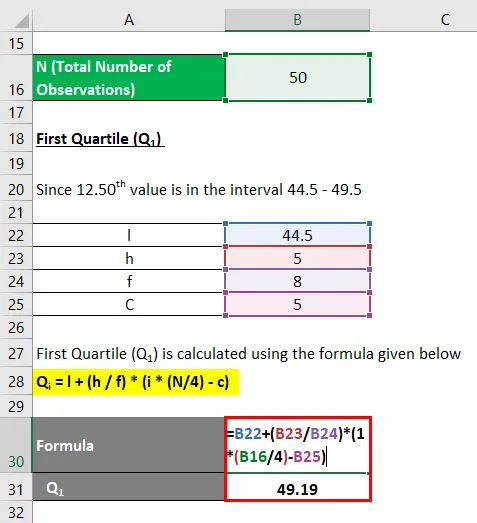
- Q 1 = (44.5 + (5/8) * (1 * (50/4) - 5)
- Q 1 = 44.5 + 4.6875
- Q 1 = 49, 19
El tercer cuartil (Q 3 ) se calcula utilizando la fórmula que se proporciona a continuación
Tercer cuartil (Q 3 )
Q i = (i * (N) / 4) th obsevation
Q1 = (i * (N) / 4) th obsevation
- Q 3 = (3 * (50) / 4) th obsevation
- Q 3 = 37.50 a obsevación
Dado que el valor 37.50 está en el intervalo (59.5 - 64.5)
Por lo tanto, el grupo de Q3 es (59.5 - 64.5)
Q i = l + (h / f) * (i * (N / 4) - c)
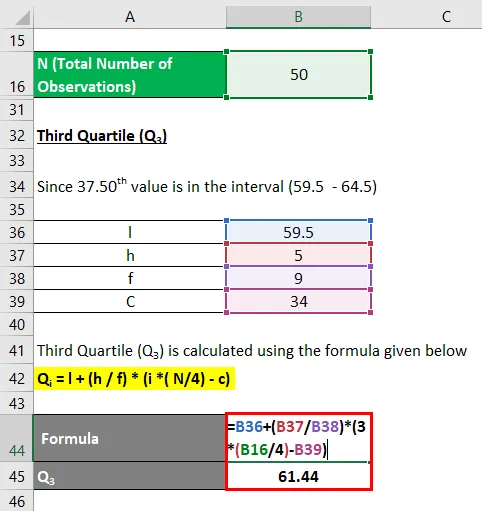
- Q 3 = 59.5 + (5/9) * (3 * (50/4) - 34)
- Q 3 = 59.5 + 1.944
- Q 3 = 61.44
Al poner los valores en las fórmulas de desviación del cuartil y coeficiente de desviación del cuartil obtenemos:
La desviación del cuartil se calcula utilizando la fórmula que se proporciona a continuación.
Desviación del cuartil = (Q 3 - Q 1 ) / 2
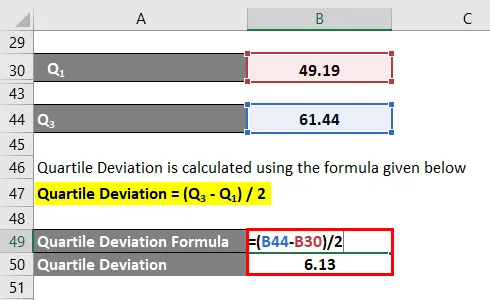
- Desviación del cuartil = (61.44 - 49.19) / 2
- Desviación del cuartil = 6.13
El coeficiente de desviación del cuartil se calcula utilizando la fórmula que se proporciona a continuación
Coeficiente de desviación del cuartil = (Q 3 - Q 1 ) / (Q 3 + Q 1 )
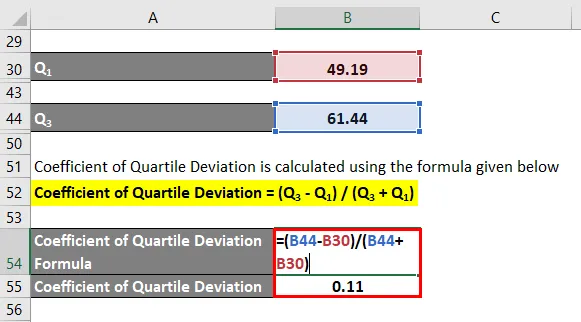
- Coeficiente de desviación del cuartil = (61.44 - 49.19) / (61.44 + 49.19)
- Coeficiente de desviación del cuartil = 12.25 / 110.63
- Coeficiente de desviación del cuartil = 0.11
Explicación
La desviación del cuartil es la dispersión en el medio de los datos donde define la propagación de los datos. Como sabemos, la diferencia entre el tercer cuartil y el primer cuartil se llama rango intercuartil y la mitad del rango intercuartil se llama semiintercuartil, que también se conoce como desviación cuartil. Ahora, podemos calcular la desviación del cuartil para los datos agrupados y no agrupados mediante el uso de una fórmula a continuación.
Desviación del cuartil = (tercer cuartil - primer cuartil) / 2
Desviación del cuartil = (Q 3 - Q 1 ) / 2
Si bien el coeficiente de desviación del cuartil se usa para comparar la variación entre dos conjuntos de datos .6687 Además, la desviación del cuartil no se ve afectada por los valores extremos donde contiene valores extremos. Un coeficiente de desviación del cuartil se puede calcular de tal manera.
Coeficiente de desviación del cuartil = (Q 3 - Q 1 ) / (Q 3 + Q 1 )
El concepto de desviación del cuartil y el coeficiente del cuartil se pueden explicar con la ayuda de un ejemplo en un conjunto definido de pasos.
Paso 1: obtenga un conjunto de datos desagrupados
En la declaración del problema, hemos considerado carreras anotadas por un bateador en los últimos 20 partidos de prueba: 96, 70, 100, 89, 78, 56, 45, 78, 68, 42, 66, 89, 90, 54, 44, 67, 87, 90, 97 y 98
Paso 2 : Organice los datos en orden ascendente:
42, 44, 45, 54, 56, 66, 67, 68, 70, 78, 78, 87, 89, 89, 90, 92, 96, 97, 98, 100
Primer cuartil ( Q 1 )
Calcule el primer cuartil
Q i = i * (n + 1) / 4 a obsevación
- Q 1 = 1 * (20 + 1) / 4 a obsevación
- Q 1 = 5.25 a obsevación
Entonces, la observación 5.25 se encuentra entre el quinto y el sexto valor en el grupo ordenado, o entre 55 y 66, por lo tanto,
- Q 1 = 55 + 0.25 * (66 - 55)
- Q 1 = 55 + 2.75
- Q 1 = 57.25
Tercer cuartil (Q 3 )
El cálculo del tercer cuartil se da como:
Q i = i * (n + 1) / 4 a obsevación
- Q 3 = i * (n + 1) / 4
- Q 3 = 3 * (20 + 1) / 4 a observación
- Q 3 = 15.75 a observación
Donde 15.75 th se encuentra entre 15 th y 16 th value en el grupo ordenado
15 a observación = 90
16ª observación = 96
- Q 3 = 90 +0.75 * (96-90)
- Q 3 = 90 + 4.5
- Q 3 = 94.5
Paso 3 : Calcule la desviación cuartil y el coeficiente de desviación cuartil sobre la base del resultado respectivo.
Desviación del cuartil = (Q 3 - Q 1 ) / 2
- Desviación del cuartil = (94.5 - 57.25) / 2
- Desviación del cuartil = 18.625
Coeficiente de desviación del cuartil = (Q 3 - Q 1 ) / (Q 3 + Q 1 )
- Coeficiente de desviación del cuartil = (94.5 - 57.25) / (94.5 +57.25)
- Coeficiente de desviación del cuartil = 0.2454
Relevancia y usos de la fórmula de desviación del cuartil
- La desviación del cuartil no tiene en cuenta puntos mucho más extremos de la distribución.
- QD también cambia con respecto al cambio de escala de datos.
- Es la mejor medida para el sistema abierto.
- Menos afectado por las fluctuaciones de muestreo en el conjunto de datos
- Dependerá únicamente de los valores centrales en la distribución.
Calculadora de fórmula de desviación cuartil
Puede usar la siguiente calculadora de fórmula de desviación del cuartil
| Q 3 | |
| Q 1 | |
| Desviación del cuartil | |
| Desviación del cuartil = |
|
|
Artículos recomendados
Esta es una guía para la fórmula de desviación del cuartil. Aquí discutimos cómo calcular la fórmula de desviación del cuartil junto con ejemplos prácticos. También proporcionamos una calculadora de desviación del cuartil con una plantilla de Excel descargable. También puede consultar los siguientes artículos para obtener más información:
- Ejemplo de fórmula de tasa de interés real
- Fórmula de ingresos por ventas
- Fórmula para cuota de mercado
- ¿Cómo calcular las ventas netas?