
F-Test Formula (Tabla de contenido)
- Fórmula
- Ejemplos
¿Qué es la fórmula F-Test?
La prueba F es una prueba estadística que nos ayuda a encontrar si dos conjuntos de población que tienen una distribución normal de sus puntos de datos tienen la misma desviación estándar o varianzas. Pero lo primero y más importante para realizar la prueba F es que los conjuntos de datos deben tener una distribución normal. Esto se aplica a la distribución F bajo la hipótesis nula. La prueba F es una parte muy crucial del Análisis de varianza (ANOVA) y se calcula tomando proporciones de dos varianzas de dos conjuntos de datos diferentes. Como sabemos que las variaciones nos dan la información sobre la dispersión de los puntos de datos. La prueba F también se usa en varias pruebas como el análisis de regresión, la prueba de Chow, etc.
Fórmula PARA la prueba F:
No existe una fórmula simple para la prueba F, pero es una serie de pasos que debemos seguir:
Paso 1: para realizar una prueba F, primero tenemos que definir la hipótesis nula y la hipótesis alternativa. Estos están dados por: -
- H0 (hipótesis nula): varianza del primer conjunto de datos = varianza de un segundo conjunto de datos
- Ha: varianza del primer conjunto de datos <varianza del segundo conjunto de datos (para una prueba inferior de una cola)
- Ha: varianza del primer conjunto de datos> varianza de un segundo conjunto de datos (para una prueba de una cola superior)
- Ha: varianza del primer conjunto de datos ≠ Varianza de un segundo conjunto de datos (para una prueba de dos colas)
Paso 2: Lo siguiente que tenemos que hacer es que necesitamos encontrar el nivel de significancia y luego determinar los grados de libertad tanto del numerador como del denominador. Esto nos ayuda a determinar sus valores críticos. El grado de libertad es el tamaño de la muestra -1.
Paso 3: Fórmula de prueba F:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
Paso 4: Encuentre el valor crítico F de la tabla F tomando un grado de libertad y un nivel de significancia.
Paso 5: Compare estos dos valores y si un valor crítico es menor que el valor F, puede rechazar la hipótesis nula.
Ejemplos de fórmula de prueba F (con plantilla de Excel)
Tomemos un ejemplo para comprender el cálculo de la prueba F de una mejor manera.
Puede descargar esta plantilla F-TEST Formula Excel aquí - Plantilla F-TEST Formula ExcelFórmula de prueba F - Ejemplo # 1
Digamos que tenemos dos conjuntos de datos A y B que contienen puntos de datos diferentes. Realice la prueba F para determinar si podemos rechazar la hipótesis nula con un nivel de significación del 1%.
Conjuntos de datos:
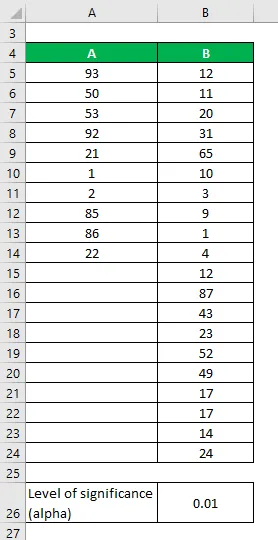
Solución:
Hipótesis nula: varianza de A = varianza de B
Grado de libertad se calcula como
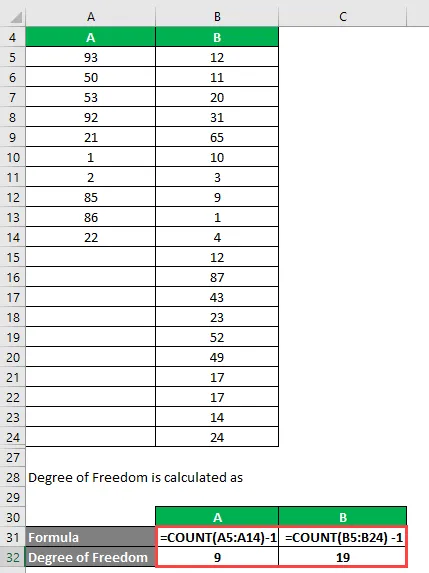
Grado de libertad
- Para A = 10 - 1 = 9
- Para B = 20 - 1 = 19
La variación se calcula como:

- Varianza de A = 1385.61
- Varianza de B = 521.22
El valor F se calcula utilizando la fórmula que se proporciona a continuación
Valor F = Variación del primer conjunto de datos / Variación del segundo conjunto de datos
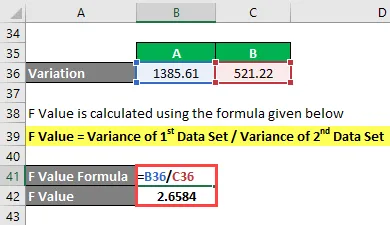
- Valor F = 1385.61 / 521.22
- Valor F = 2.6584
Mesa F:
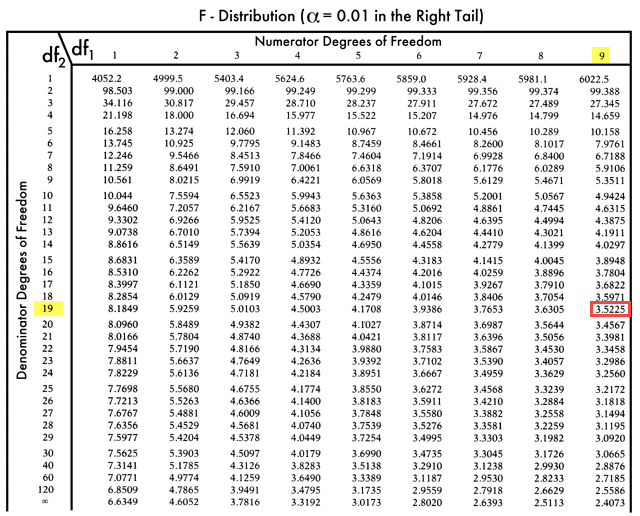
Entonces F valor crítico = 3.5225
Como F crítico es mayor que el valor F, no podemos rechazar la hipótesis nula.
Fórmula de prueba F - Ejemplo # 2
Suponga que está trabajando en una empresa de investigación y desea conocer el nivel de emisión de óxido de carbono de 2 marcas diferentes de cigarrillos y si son significativamente diferentes o no. En su análisis, ha recopilado la siguiente información:
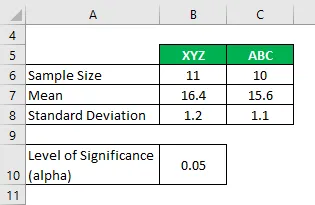
Solución:
Grado de libertad se calcula como
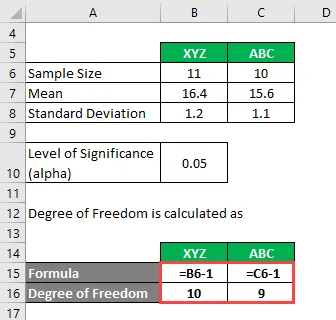
Grado de libertad
- Para XYZ = 11 - 1 = 10
- Para ABC = 10 - 1 = 9
La variación se calcula como:
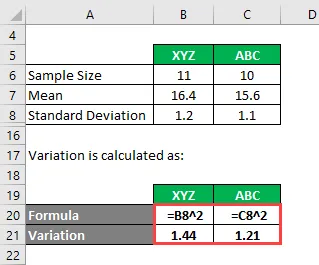
- Varianza de XYZ = 1.2 2 = 1.44
- Varianza de ABC = 1.1 2 = 1.21
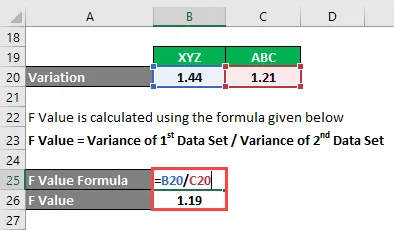
- Valor F = 1.44 / 1.21
- Valor F = 1.19
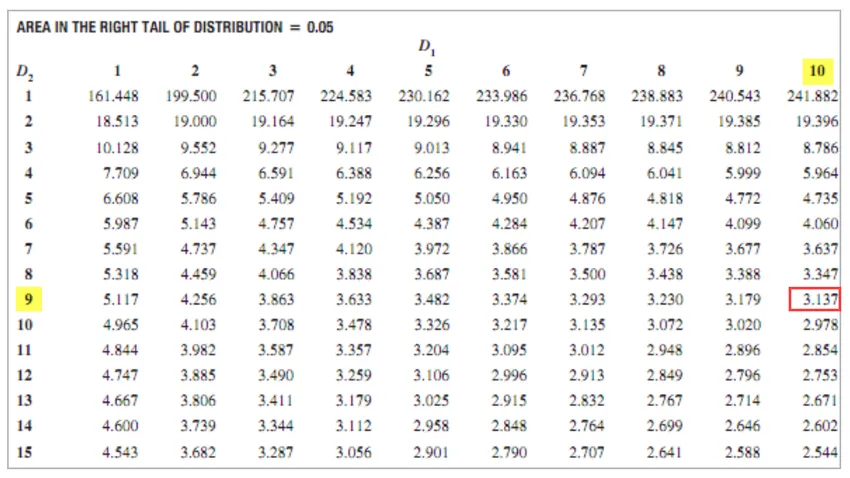
F Valor crítico = 3.137
Dado que el valor F crítico> F, la hipótesis nula no puede ser rechazada.
Explicación
En los ejemplos anteriores, hemos visto la aplicación de F-Test y cómo se realiza. Pero hay un conjunto de suposiciones que debemos tener cuidado antes de realizar la prueba F; de lo contrario, no obtendremos los resultados requeridos:
- Lo primero es que debemos colocar siempre el numerador de mayor valor de varianza al calcular el valor de F. Entonces, si F = V1 / V2, V1 debería ser> V2
- Si queremos realizar una prueba de 2 colas, necesitamos dividir el nivel de significancia entre 2 y ese será el nivel correcto para encontrar el valor crítico
- Solo usamos la varianza es el cálculo del valor F y si nos dan desviaciones estándar, como en el ejemplo 2, deben ser al cuadrado para encontrar la varianza.
- Tanto las muestras deben ser independientes entre sí y el tamaño de la muestra debe ser inferior a 30
- Los conjuntos de población de los que se extraen las muestras deben distribuirse normalmente
Estos son los parámetros / supuestos clave que deben tenerse en cuenta al realizar la prueba F.
Relevancia y uso de la fórmula F-Test
La prueba F, como se discutió anteriormente, nos ayuda a verificar la igualdad de las dos variaciones de población. Entonces, cuando tenemos dos muestras independientes que se extraen de una población normal y queremos verificar si tienen o no la misma variabilidad, utilizamos la prueba F. La prueba F también tiene una gran relevancia en el análisis de regresión y también para probar la importancia de R 2 . En pocas palabras, F-Test es una herramienta muy importante en estadística si queremos comparar la variación de 2 o más conjuntos de datos. Pero uno debe tener en cuenta todos los supuestos antes de realizar esta prueba.
Artículos recomendados
Esta ha sido una guía para la F-Test Formula. Aquí discutimos cómo calcular la prueba F junto con ejemplos prácticos y una plantilla de Excel descargable. También puede consultar los siguientes artículos para obtener más información:
- Fórmula de distribución T
- Fórmula para fijación de precios de bonos
- Fórmula de porcentaje de error
- Cálculo de la fórmula NOPAT