Análisis de varianza de una sola vía
El análisis de varianza escrito en breve como ANOVA es el procedimiento mediante el cual podemos comparar medias en tres o más poblaciones. Estadísticamente, enmarcamos dos hipótesis, la hipótesis nula: "Todas las medias de población son iguales" y la hipótesis alternativa: "No todas las medias de población son iguales". Nos permite probar la igualdad de medias múltiples en una prueba en lugar de comparar dos medias a la vez, lo cual no es factible cuando hay varios grupos. En este tema, vamos a aprender sobre One Way ANOVA en R.
El análisis de varianza unidireccional nos ayuda a analizar solo un factor o variable. Por ejemplo, existen cinco regiones y queremos verificar si las precipitaciones medias diarias para las cinco regiones son iguales o si son diferentes. En este caso, solo hay un factor que es la región, ya que debemos verificar si los factores regionales afectan la recepción de lluvia y el patrón.
Suposiciones de análisis de varianza
Los siguientes son los supuestos que deben cumplirse para aplicar ANOVA unidireccional:
- Las poblaciones de las que se extraen las muestras se distribuyen normalmente.
- Las poblaciones de las que se extraen las muestras tienen la misma varianza o desviación estándar.
- Las muestras extraídas de diferentes poblaciones son aleatorias e independientes.
¿Cómo funciona ANOVA unidireccional en R?
Para nuestra demostración, estamos utilizando los datos que contienen dos variables, a saber. Marca y Ventas. Hay cuatro marcas: ATB, JKV, MKL y PRQ. Se dan ventas mensuales para estas marcas. Necesitamos verificar si las ventas promedio en las cuatro marcas son iguales o si son diferentes entre sí. Para verificar esto, utilizaremos el ANOVA unidireccional. El procedimiento paso a paso para implementar ANOVA es el siguiente:
- Primero, importe los datos a R. Los datos están presentes en formato CSV. Entonces, para importarlo, usaremos la función read.csv ().

- Ver los primeros registros de los datos. Esto es importante para verificar si los datos se han importado correctamente a R. De manera similar, aplicaremos una función resumen () sobre los datos, para obtener información básica sobre los datos.

- Cada vez que usamos las variables presentes en el conjunto de datos, necesitamos mencionar explícitamente el nombre del conjunto de datos como brand_sales_data $ Brand o brand_sales_data $ Sales. Para superar esto, emplearemos la función adjuntar. La función debe aplicarse de la siguiente manera.

- Agreguemos las ventas por marca usando la media o la desviación estándar. La agregación nos ayuda a tener una idea básica de los datos.
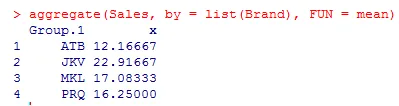
El resultado anterior muestra que los medios para los cuatro grupos diferentes no son iguales. JKV tiene las ventas medias más altas.
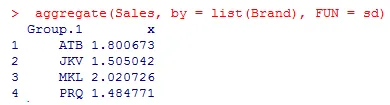
Como se puede ver arriba, las desviaciones estándar en los cuatro grupos no muestran ninguna diferencia significativa y es más alta para la marca MKL.
- Ahora, aplicaremos ANOVA para validar si las medias en las tres poblaciones son iguales o si existe alguna diferencia.
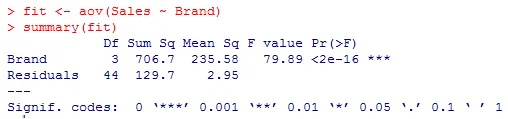
De los resultados anteriores podemos ver que la prueba ANOVA para Brand es significativa debido a p <0.0001. Podemos interpretar que todas las marcas no tienen los mismos niveles de preferencia en el mercado, lo que influye en la venta de estas marcas en el mercado. Esto podría deberse a muchos factores y al gusto de las personas por una marca en particular.
- El resultado anterior se puede visualizar y facilita la interpretación. Para eso, utilizaremos la función plotmeans () en la biblioteca gplots (). Funciona de la siguiente manera:

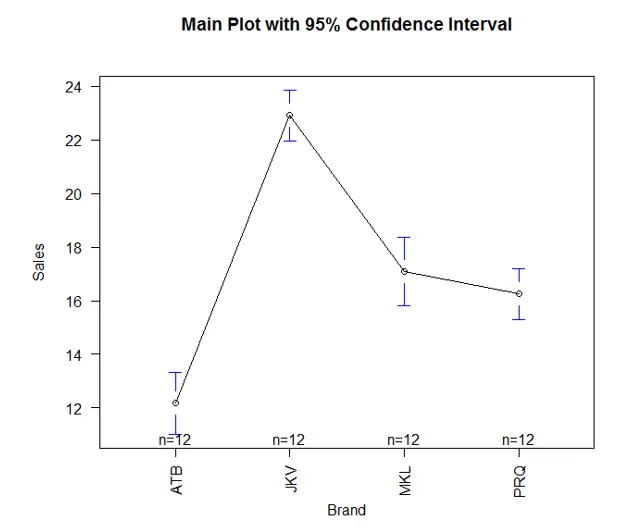
Como podemos ver arriba, la función plotmeans () en el paquete gplots nos permite comparar visualmente las medias de diferentes grupos. Podemos ver que los medios no son los mismos en las cuatro marcas. Sin embargo, los medios para las marcas MKL y PRQ caen en un rango cercano.
- El análisis anterior nos ayuda a verificar si las marcas tienen los mismos medios o no, sin embargo, es difícil hacer la comparación por pares. Podemos hacer comparaciones por pares para diferentes marcas, utilizando la función TukeyHSD () que facilita verificar si una marca es significativamente diferente de cualquiera de las restantes.

Las comparaciones por pares como arriba. La diferencia entre dos grupos cualquiera es significativa si p <0.001. Como podemos ver arriba, el valor p para el par PRQ-MKL es mucho más alto, lo que indica que las dos marcas no son significativamente diferentes entre sí.
Para visualizar las comparaciones por pares, trazaremos los resultados anteriores de la siguiente manera:

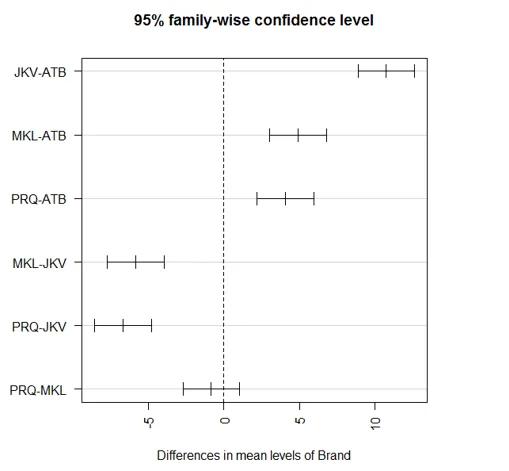
La primera función de par gira las etiquetas del eje haciéndolas horizontales, y la segunda instrucción de par ajusta los márgenes para que las etiquetas se ajusten correctamente, de lo contrario, saldrán de la pantalla.
El gráfico anterior ofrece una buena visión, pero podemos trazar los resultados en forma de diagrama de caja para obtener mejores ideas para una interpretación más clara, como se demuestra a continuación.

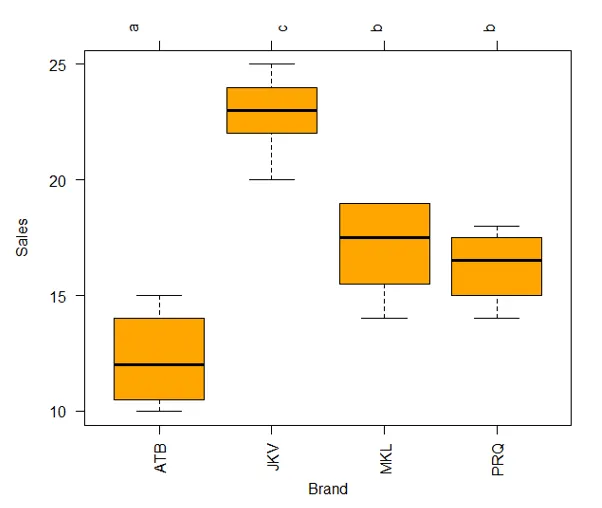
La función glht () utilizada anteriormente viene con un conjunto completo de métodos para comparar múltiples medios. Tenga en cuenta que la opción de nivel en la función cld () pertenece al nivel de significancia, por ejemplo, 0.05 o 95 por ciento de confianza)
Usando el diagrama anterior, resulta fácil comparar medias entre los grupos y también facilita la interpretación sistemática. Hay letras, en la parte superior de la trama, para cada marca. Si dos marcas tienen la misma letra, entonces no tienen medios significativamente diferentes como las marcas MKL y PRQ en este caso, que tienen la misma letra b.
- Hasta ahora, implementamos ANOVA y utilizamos gráficos para visualizar los resultados. Sin embargo, es igualmente importante probar los supuestos. Primero, validaremos el supuesto de normalidad.

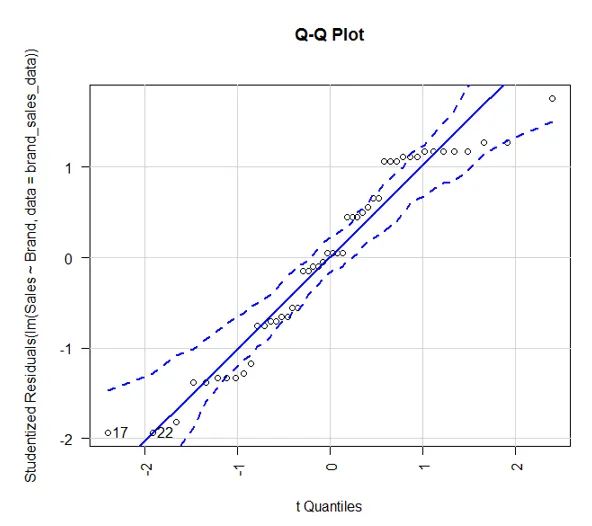
El paquete del automóvil en R proporciona la función qqPlot (). El gráfico anterior muestra que los datos caen dentro del 95% de envoltura de confianza. Esto indica que el supuesto de normalidad casi se ha cumplido.
A continuación, validaremos si las variaciones entre las marcas son iguales. Para esto, usaremos la prueba de Bartlett
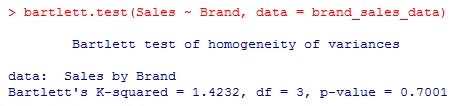
El valor p muestra que las variaciones en todo el grupo no difieren significativamente
Por último, pero no menos importante, verificaremos si hay valores atípicos que afecten los resultados de ANOVA.
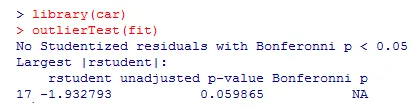
Del resultado anterior, podemos ver que no hay indicios de valores atípicos en los datos (NA ocurre cuando p> 1)
Teniendo en cuenta los resultados de QQ Plot, la prueba de Bartlett y la prueba de valores atípicos, podemos decir que los datos cumplen con todos los supuestos de ANOVA y que los resultados obtenidos son válidos.
Conclusión: ANOVA unidireccional en R
ANOVA es una técnica estadística muy útil que se puede utilizar para comparar medias en múltiples poblaciones. R ofrece una amplia gama de paquetes para implementar ANOVA, obtener resultados y validar los supuestos. En R, los resultados estadísticos se pueden interpretar en formas visuales que ofrecen información más profunda.
Artículos recomendados
Esta es una guía de ANOVA unidireccional en R. Aquí discutimos cómo funciona el ANOVA unidireccional y los supuestos del análisis de varianza. También puede echar un vistazo a los siguientes artículos para obtener más información:
- Lenguaje de programación R
- Regresión vs ANOVA
- Cómo interpretar los resultados usando la prueba ANOVA
- GLM en R