Fórmula CAPM (Tabla de contenido)
- Fórmula CAPM
- Calculadora CAPM
- Fórmula CAPM en Excel (con plantilla de Excel)
Fórmula CAPM
La relación lineal entre el rendimiento esperado de la inversión y su riesgo sistemático está representada por la fórmula del Modelo de fijación de precios de activos (CAPM).
CAPM se calcula de acuerdo con la siguiente fórmula: -
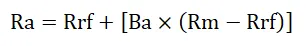
Dónde:
- Ra = retorno esperado de una inversión
- Rrf = tasa libre de riesgo
- Ba = Beta de la inversión
- Rm = retorno esperado en el mercado
Y Risk Premium es la diferencia entre el rendimiento esperado del mercado menos la tasa libre de riesgo (Rm - Rrf) .
Prima de riesgo del mercado
La prima de riesgo de mercado es el exceso de rendimiento, es decir, la recompensa que se espera que compense a un inversor por asumir el riesgo inherente a la cartera, ya que invertir en bolsa es siempre mayor que invertir en bonos del gobierno. Por lo tanto, es una diferencia entre el rendimiento esperado del mercado y la tasa libre de riesgo. La tasa de rendimiento del mercado, Rm, se puede estimar con base en rendimientos pasados o rendimientos futuros proyectados. Por ejemplo, los bonos y letras del tesoro de los Estados Unidos se utilizan para la tasa libre de riesgo.
Rendimiento esperado
La "Ra" se refiere al rendimiento esperado de una inversión durante el período de tiempo.
Tasa libre de riesgo
El "Rrf" denota la tasa libre de riesgo, que es igual al rendimiento de una letra del Tesoro de los Estados Unidos a 10 años o un bono del gobierno. La tasa libre de riesgo es el rendimiento de una inversión que no genera ningún riesgo, pero en el mundo real incluye el riesgo de inflación. La tasa libre de riesgo también debe ser del país donde se realiza la inversión, y el período de vencimiento del bono también debe coincidir con el período de tiempo de la inversión. Normalmente, la tasa de rendimiento libre de riesgo que se utiliza para estimar la prima de riesgo suele ser el promedio de las tasas de rendimiento libres de riesgo históricas y no generalmente la tasa de rendimiento libre de riesgo actual.
Beta
La beta que se representa como "Ba" en las fórmulas de CAPM es una medida de la volatilidad de un valor o una cartera y se calcula midiendo cuánto cambia el precio de las acciones con el rendimiento del mercado general. Beta es una medida de riesgo sistemático. Por ejemplo, si la beta de una empresa es igual a 1.7, significa que tiene un 170% de la volatilidad de los retornos del promedio del mercado y los movimientos de los precios de las acciones serán bastante extremos. Si la beta es igual a 1, el rendimiento esperado de la inversión es igual al rendimiento del promedio del mercado. Si la beta es -1, significa que los precios de las acciones son menos riesgosos y volátiles.
Aplicación del modelo CAPM
Veremos algunos ejemplos de CAPM que se utilizan con mayor frecuencia para determinar cuál debería ser el precio justo de una inversión. Cuando calculamos la tasa de rendimiento del activo riesgoso utilizando CAPM, esa tasa también puede usarse para descontar los flujos de efectivo futuros de la inversión a su valor presente y finalmente llegar al precio justo de la inversión.
Ejemplos de fórmula CAPM
Tomemos un ejemplo para descubrir el CAPM para una empresa: -
Puede descargar esta plantilla CAPM Formula Excel aquí - Plantilla CAPM Formula ExcelEjemplo 1
Digamos que se espera que la Acción A genere retornos del 14% durante el próximo año y que la tasa actual libre de riesgo sea del 6%, y que desee calcular si es rentable invertir en esto. Ha calculado el valor beta de la acción, que es 1.7. El mercado de valores en general tiene una beta de 1.0. Esto implica que la acción conlleva un mayor nivel de riesgo que el riesgo general. Por lo tanto, esperamos un rendimiento más alto que el rendimiento anticipado del 14% del mercado para el próximo año.
El rendimiento esperado se puede calcular de la siguiente manera:
- Retorno requerido (Ra) = Rrf + (Ba * (Rm - Rrf))
- Retorno requerido (Ra) = 6% + 1.7 * (14% - 6%)
- Retorno requerido (Ra) = 6% + 13.6%
- Retorno requerido (Ra) = 19.6%
Este cálculo le indica que obtendrá un 19, 6% de su inversión.
Ejemplo 2
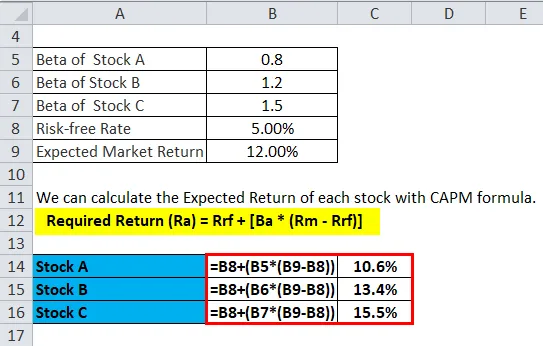
Supongamos que un inversor está pensando en invertir en una de las tres acciones disponibles en el mercado. La siguiente información está disponible para estimar la tasa de rendimiento de las tres acciones.
- Stock A con una beta de 0.80
- Stock B con una beta de 1.20
- Stock C con una beta de 1.50
La tasa libre de riesgo es de 5.00% y el rendimiento esperado del mercado es de 12.00%.
Podemos calcular el rendimiento esperado de cada acción con la fórmula CAPM.
- Retorno requerido (Ra) = Rrf + (Ba * (Rm - Rrf))
Retorno esperado de stock A
- E (R A ) = 5.0% + 0.80 * (12.00% - 5.0%)
- E (R A ) = 5.0% + 5.6%
- E (R A ) = 10, 6%
Retorno esperado de stock B
- E (R B ) = 5.0% + 1.20 * (12.00% - 5.0%)
- E (R B ) = 5.0% + 8.4%
- E (R B ) = 13, 4%
Retorno esperado de stock C
- E (R C ) = 5.0% + 1.50 * (12.00% - 5.0%)
- E (R C ) = 5.0% + 10.5%
- E (R C ) = 15, 5%
Por lo tanto, vemos que es mejor invertir en acciones C. Por lo tanto, se ve que cuanto mayor sea la beta, mayor será el rendimiento esperado de acuerdo con la fórmula CAPM.
Ejemplo 3
Ahora veremos un problema de aplicación del rendimiento esperado. Podemos calcular el valor actual neto utilizando el rendimiento esperado o la tasa de obstáculo de la fórmula CAPM como una tasa de descuento para estimar el valor actual neto de una inversión
Se proporciona la siguiente información:
- β = 1.3
- Rrf = 6%
- Rm = 13%
Por lo tanto, la tasa de obstáculos o el rendimiento esperado del proyecto se calcula de la siguiente manera:
- Retorno requerido (Ra) = Rrf + (Ba * (Rm - Rrf))
- Ra = 6% + 1.3 * (13% - 6%)
- Ra = 6% + 9.1%
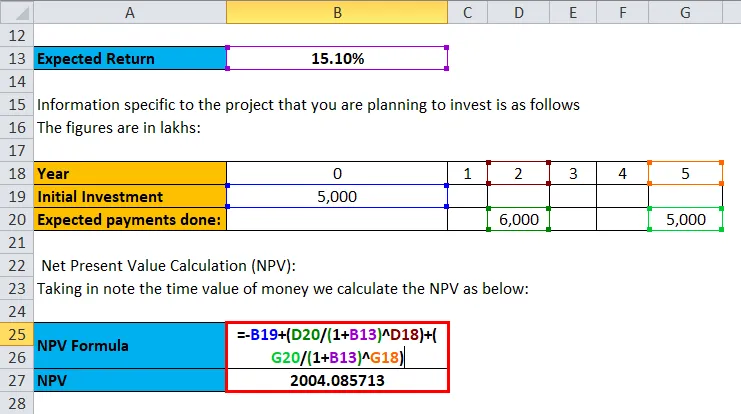
- Ra = 15, 1%
La información específica del proyecto que planea invertir es la siguiente. Las cifras están en lakhs:
- Inversión inicial = ₹ 5, 000
- Pagos previstos realizados: ₹ 6, 000 en el 2º año, ₹ 5, 000 en el 5º año
Cálculo del valor actual neto (VPN): tomando en cuenta el valor temporal del dinero calculamos el VPN de la siguiente manera:
Npv = - inversión inicial + suma de (valor de inversión / (tasa de 1+) no. De años)
Entonces, la inversión inicial es de 5000, y luego se invierte 6000 en el segundo año y 5000 en el 5to año. solo pon los valores para obtener los resultados
- VPN = -5, 000 + (6, 000 / 1.151 2) + (5000 / 1.151 5)
- VPN = ₹ 2004.085713
Por lo tanto, el valor neto de la inversión realizada es ₹ 2004.085713.
Suposiciones de la fórmula CAPM
- Los inversores mantienen la diversificación en una gama de inversiones para eliminar el riesgo no sistemático.
- Los inversores pueden prestar y pedir prestado cualquier cantidad bajo la tasa libre de riesgo.
- CAPM considera que un mercado es ideal y no incluye impuestos ni ningún costo de transacción en una cuenta.
- Suponga que toda la información está disponible al mismo tiempo para todos los inversores.
- Todo inversor se opone a la exposición al riesgo.
Limitaciones
La limitación de esta fórmula CAPM es que cuanto mayor es el riesgo del activo, mayor es el rendimiento esperado, que no siempre es cierto.
Calculadora de fórmulas CAPM
Puede usar la siguiente calculadora CAPM
| Rrf (%) | |
| Licenciado en Letras | |
| Rm (%) | |
| Real academia de bellas artes | |
| Ra = Rrf + (Ba X (Rm - Rrf)) |
| 0 + (0 X (0-0)) = 0 |
Fórmula CAPM en Excel (con plantilla de Excel)
Aquí haremos el mismo ejemplo de la fórmula CAPM en Excel. Es muy fácil y simple. Debe proporcionar las tres entradas, es decir , tasa libre de riesgo, beta de la inversión y rendimiento esperado en el mercado
Puede calcular fácilmente el CAPM utilizando Fórmula en la plantilla proporcionada.
El rendimiento esperado se puede calcular de la siguiente manera:
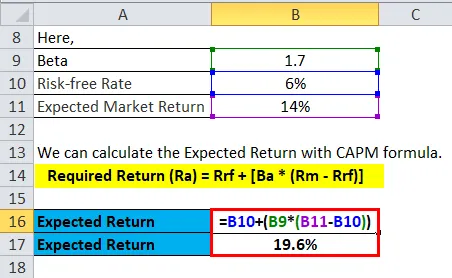
Podemos calcular el rendimiento esperado de cada acción con la fórmula CAPM.
El retorno esperado del proyecto se calcula de la siguiente manera:

El valor neto de la inversión se calcula como:
Artículos recomendados
Esta ha sido una guía para una fórmula CAPM. Aquí discutimos sus usos junto con ejemplos prácticos. También le proporcionamos la Calculadora CAPM con una plantilla de Excel descargable. También puede consultar los siguientes artículos para obtener más información:
- Fórmula para el ratio de deuda
- Guía para la fórmula de rendimiento fiscal equivalente
- Ejemplos de fórmula de precio a ganancias
- Fórmula de retorno de activos promedio