
Introducción a la fusión Ordenar en JavaScript
Los algoritmos de clasificación son muy importantes en informática. El resultado de la ordenación es organizar los elementos de una lista en un cierto orden (ya sea ascendente o descendente). Merge Sort in JavaScript es uno de los algoritmos de clasificación más eficientes disponibles, ya que se basa en el concepto de divide y vencerás. Como su nombre indica, primero divida el problema más grande en problemas pequeños que resuelva los problemas más pequeños para resolver el problema más grande. Conceptualmente, Merge sort es una combinación de dos algoritmos básicos llamados MERGE y MERGE_SORT.
que funciona de la siguiente manera:
- Divida la lista sin ordenar en n cantidad de sublistas de un solo elemento (n es la cantidad total de elementos en la lista sin clasificar).
- Combine repetidamente sublistas en sublistas ordenadas hasta que solo haya una lista ordenada.
Implementación de Merge Sort en JavaScript
El algoritmo MERGE sigue el procedimiento de combinar dos listas ordenadas en una lista ordenada.
Ejemplo: supongamos que hay dos listas, es decir, la Lista 1 (1, 5, 3) y la Lista 2 (7, 2, 9).
1. Primero ordene ambas listas.
Ahora, veremos y aplicaremos la técnica E en él.
2. Luego, crearemos una nueva lista de tamaño x + y donde x es el número de elementos en la Lista 1 e y es el número de elementos en la Lista 2.

En nuestro caso x = 3 e y = 3, entonces x + y = 6.
3. Ahora, tenemos dos punteros.
Un primer puntero apuntando a la primera posición de la Lista 1 y un Segundo puntero apuntando a la primera posición de la Lista 2.

4. Luego compararemos el valor de ambos punteros. El puntero con menor valor, copie ese elemento en la Lista 3 y mueva el puntero a la derecha de la lista con un valor menor y la lista resultante (es decir, Lista 1 y Lista 3)

5. Del mismo modo, realice el paso 4 una y otra vez.

Más recorrido …
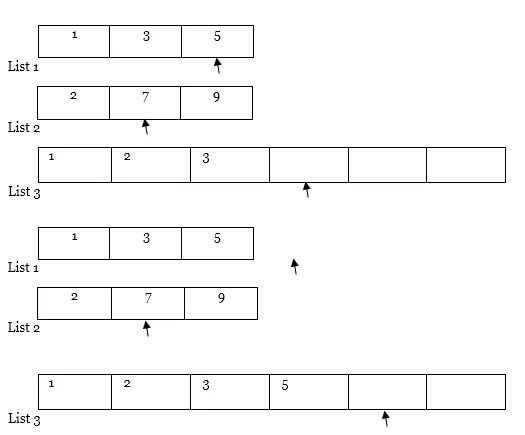
Nota : Si una de las listas (es decir, la lista 1 o la lista 2) se recorre por completo como en el caso, copie todo el contenido de otra lista desde el puntero a la lista de resultados (es decir, la lista 3) de la siguiente manera.

Pseudocódigo
Function merge (sublist1, sublist2) (
Create var for result list
While sublist1 length > 0 and sublist2 length > 0
If sublist1(0) < sublist2(0) Copy the sublist1 pointer value to result list and Shift pointer of sublist1 to right
else
Copy the sublist2 pointer value to result list and Shift pointer of sublist2 to right
Return concat sublist1 or sublist2 (depending if node1 is empty or not)
El algoritmo MERGE_SORT divide la lista sin clasificar dada al tamaño mínimo y luego llama al algoritmo MERGE para combinar la lista en la nueva lista ordenada.
Pseudocódigo
function mergeSort(list) (
If list length < 2
Return list
Create var for middle index of list
Create var for left index of list
Create var for right index of list
Recursively call mergeSort function
)
Ejemplo
Aquí estamos siguiendo la implementación de clasificación de fusión de arriba hacia abajo. Comienza en la parte superior y continúa hacia abajo, con cada turno recursivo haciendo la misma pregunta "¿Qué se debe hacer para ordenar la lista?" Y la respuesta es "Divida la lista en dos, haga una llamada recursiva y combine el resultados ".
Código en Javascript
// Split the list into halves and merge them recursively
function mergeSort (list) (
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
var mid = Math.floor(list.length / 2);
var left = mergeSort(list.slice(0, mid));
var right = mergeSort(list.slice(mid));
return merge(left, right);
)
// compare the lists element by element and return the concatenated resultList
function merge (sublist1, sublist2) (
var resultList = ();
while (sublist1.length > 0 && sublist2.length > 0)
resultList.push(sublist1(0) < sublist2(0)? sublist1.shift() : sublist2.shift());
return resultList.concat(sublist1.length? sublist1 : sublist2);
)
const list = (6, 5, 3, 1, 8, 7, 2, 4, 2, 5, 1, 2, 3) console.log(mergeSort(list)) //( 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 6, 7, 8 )
La función principal del tipo de fusión dividirá la lista dada en listas más pequeñas en cada iteración de la llamada recursiva. No olvide que la recursividad requiere la condición base para evitar una recursión infinita. En nuestro caso, tenemos:
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
Después de configurar la condición base para la recursividad, identificaremos el índice intermedio para dividir la lista dada en la sublista izquierda y derecha, como puede ver arriba en el diagrama de ejemplo. Luego, necesitamos fusionar la sublista izquierda y la sublista derecha que veremos ahora. En la función de fusión anterior, debemos asegurarnos de que estamos ordenando todos los elementos en la sublista izquierda y la sub- lista derecha. lista. La forma en que haremos esto es mediante el uso de un bucle while. Dentro del ciclo while, compararemos el elemento en la sublista izquierda y el elemento en la sublista derecha uno por uno. Podemos empujar el más pequeño de los dos a la lista de resultados y mover el cursor de la sublista izquierda y la sublista derecha en consecuencia. Finalmente, necesitamos concatenar la lista de resultados. ¡Esto es muy importante! Si no hacemos este último paso aquí, tendremos una lista incompleta de elementos al final porque la condición del bucle while fallará una vez que cualquiera de los dos punteros llegue al final.
Salida:

Propiedades del orden de fusión
- La ordenación por fusión es estable ya que el mismo elemento en una matriz mantiene sus posiciones originales entre sí.
- La ordenación por fusión no está 'en su lugar' ya que durante la fusión crea una copia de toda la lista. Debido a esto, la complejidad del espacio (O (n)) de este algoritmo es en realidad mayor que otros, y no debe usarse en problemas complejos donde el espacio es premium.
- La complejidad de tiempo general de la clasificación de combinación es O (nLogn). Es más eficiente ya que también lo es en el peor de los casos, el tiempo de ejecución es O (nlogn).
Conclusión
Combinar las complejidades de tiempo mejores, peores y de caso promedio son las mismas, lo que lo convierte en un algoritmo más eficiente. Funciona más rápido que otras técnicas de clasificación. La ordenación por fusión se puede aplicar a archivos de cualquier tamaño. Es altamente paralelizable debido al uso del método de divide y vencerás. Con el fin de desarrollar conceptos básicos sólidos en ciencias de la computación, se recomienda comprender a fondo diferentes algoritmos de clasificación.
Artículo recomendado
Esta ha sido una guía para Combinar Ordenar en JavaScript. Aquí discutimos Introducción a la fusión Ordenar en JavaScript y la implementación junto con Propiedades. También puede consultar nuestros otros artículos sugeridos para obtener más información:
- Funciones matemáticas de JavaScript
- Introducción a JavaScript
- Mejores marcos de Javascript
- Herramientas de JavaScript
- Los 6 mejores algoritmos de clasificación en JavaScript