
Introducción a la serie Fibonacci en Python
Serie Fibonacci en Python, esto se conoce como una serie de números, donde el siguiente número es la suma de los dos números actuales.
Por ejemplo:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. así sucesivamente
Entonces aquí 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 y así sucesivamente.
Mirando lo anterior, uno tendría cierta idea de lo que estamos hablando.
Sin embargo, en términos de regla matemática, se puede escribir como:

Donde enésimo número es la suma del número en los lugares (n-1) y (n-2). Cuando se trata de implementar la serie Fibonacci, podría haber una serie de lenguajes de codificación a través de los cuales podría hacerse.
Sin embargo, Python es un lenguaje ampliamente utilizado hoy en día. Veamos la implementación de la serie Fibonacci a través de Python. Uno debe estar al tanto de las declaraciones de condicionamiento básicas como el bucle, if-else, while loop, etc. en Python, antes de continuar aquí. Si no, sería genial si uno puede revisarlo y luego retomar el contenido que viene. Aquí, para fines de demostración, estoy usando Spyder, que es IDE para el lenguaje de programación Python. También se puede usar cualquier otra computadora portátil IDE o Ipython para la ejecución de los programas Python.
Serie Fibonacci en Python
Veamos la implementación del número de Fibonacci y la serie considerando que los dos primeros elementos de Fibonacci son 0 y 1:
Sin embargo, puede ajustar la función de Fibonacci según sus necesidades, pero primero vea los conceptos básicos y pase gradualmente a otros.
Código de Python para encontrar el enésimo número de Fibonacci
Código 1:
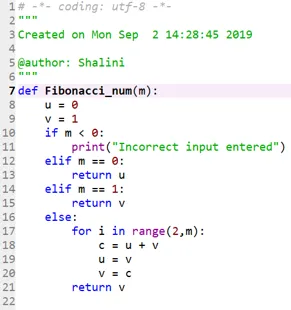
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Código 2:
Salida:
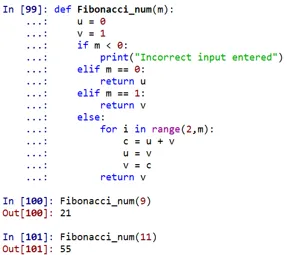
Como se puede ver, el número de Fibonacci en el 9 ° lugar sería 21, y en el 11 ° lugar sería 55.
- Aquí "fibonacci_num" es una función definida, que se encarga de encontrar el número de Fibonacci con la ayuda de ciertas condiciones. Se puede llamar a esta función especificando cualquier posición.
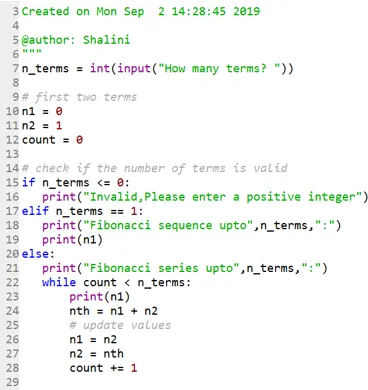
Ahora veamos cómo se pueden imprimir series hasta la posición mencionada:
Código:
Salida:
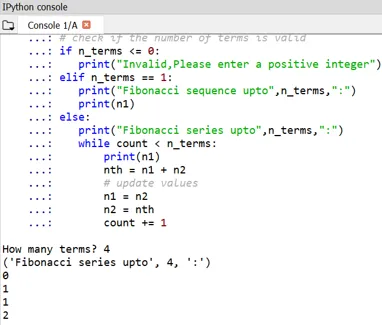
Uno puede notar que el inicio de los números de Fibonacci se define como 0 y 1.
- Si alguien quiere definir sus propios términos iniciales, eso también se puede hacer de la misma manera ajustando n1 y n2. Aquí está el ejemplo para eso:
Digamos ahora que queremos que nuestros términos iniciales sean: n1 = 3, n2 = 5
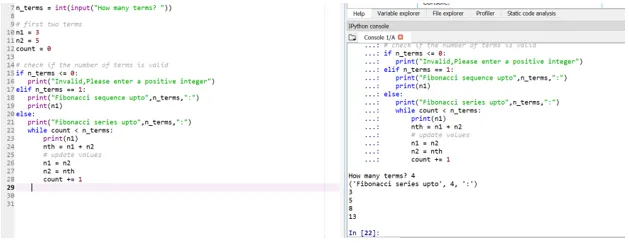
Por lo tanto, aquí su posición del 4º término (se toma la entrada del usuario), se decidirá en función de sus términos iniciales.
Métodos a través de los cuales se puede generar la serie Fibonacci
A continuación se presentan los tres métodos, a través de los cuales se pueden generar series de Fibonacci:
1. A través de generadores
Código:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Salida:
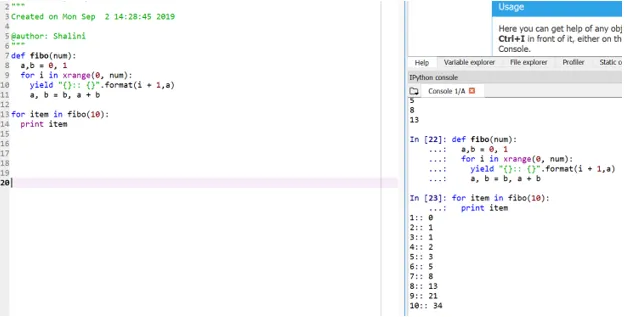
Este método se conoce como "generador" porque la función xrange es un generador de los números entre 0 y num y el rendimiento es el generador para la salida formateada.
Esto es lo que xrange hace por ti:

Aquí, la serie de Fibonacci se ha definido en forma de función, dentro de la cual la función loop, xrange y yield se encarga de la salida.
2. A través del bucle
Código:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Salida:

Como se puede ver, se ha usado simple for loop para imprimir la serie de Fibonacci entre 0 y 10. En el interior de loop, se han asignado nuevos valores a las variables. U y v son los valores iniciales predeterminados de Fibonacci que se han establecido en 0 y 1 respectivamente.
A medida que se ejecuta el ciclo, el nuevo valor de u es el antiguo valor de v, mientras que el nuevo valor de v es la suma de los antiguos valores de u y v. Esto continúa hasta el final del rango de valores.
3. A través de la recursión
Código:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Salida:
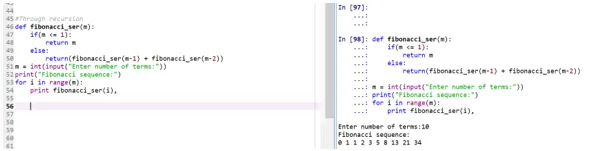
- La función "fibonacci_ser" está haciendo la llamada a sí mismo para imprimir la serie Fibonacci.
- Y de ahí que el método tenga su nombre de "recursión".
Pasos seguidos aquí:
- Aquí se le ha pedido al usuario que ingrese el lugar hasta el cual se necesita imprimir la serie Fibonacci.
- El número pasa por la función "fibonacci_ser".
- La condición se verifica si la longitud proporcionada es inferior a 1 o no. En caso afirmativo, el resultado se da de inmediato.
- Sin embargo, si la longitud es mayor que 1, se realizan llamadas recursivas a "fibonacci_ser" con argumentos que tienen una longitud menor que 1 y 2, es decir, fibonacci_ser (m-1) y fibonacci_ser (m-2).
- Por lo tanto, la recursividad da el resultado deseado e imprime.
- En resumen, discutimos tres formas de mostrar la serie de Fibonacci.
- A través del bucle for, a través de generadores y a través de la recursividad.
Los tres códigos de Python resumidos
A continuación se muestran los tres códigos de Python:
1. A través de generadores
Código:
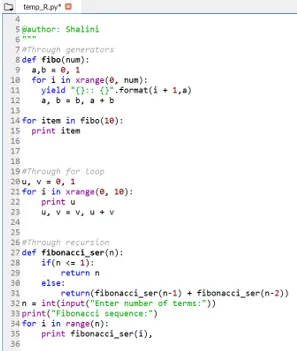
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. A través del bucle
Código:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. A través de la recursión
Código:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
A continuación se resumen todos los procedimientos, uno debe practicar para tener un buen control de todos.
Salida:
Conclusión
Al revisar el contenido anterior de Fibonacci, uno tendría una comprensión nítida de los números y series de Fibonacci, especializados en python. Una vez, uno se siente cómodo con la lógica de la serie Fibonacci, generar otro conjunto de series, trabajar con otros números y con varios métodos ahora será un juego de niños para usted. Un enfoque lógico es la única forma de sobresalir en esto.
Artículos recomendados
Esta es una guía de la serie Fibonacci en Python. Aquí discutimos los números y series de Fibonacci, especializados en python, generando otro conjunto de series, trabajando con otros números y con varios métodos. También puede consultar nuestros otros artículos relacionados para obtener más información:
- Generador de números aleatorios en Python
- Funciones matemáticas en Python
- Factorial en Python
- Encapsulación en Python
- Serie Fibonacci en Java
- Características de Python
- Programa Factorial en JavaScript
- Generador de números aleatorios en Matlab
- Generador de números aleatorios en C #
- Encapsulación en JavaScript