
Diferencia entre puntaje Z vs puntaje T
El puntaje Z es una conversión de datos sin procesar a un puntaje estándar, cuando la conversión se basa en la media y la desviación estándar de la población. Cuando un conjunto de datos completo está disponible con nosotros, podemos calcular el puntaje Z. El puntaje Z es la resta de la media de la población del puntaje bruto y luego divide el resultado con la desviación estándar de la población. El puntaje T es una conversión de datos sin procesar al puntaje estándar cuando la conversión se basa en la media muestral y la desviación estándar muestral. Cuando el conjunto de datos de población no está disponible, entonces tenemos que recoger algunos datos de muestra para calcular la media muestral y la desviación estándar de la población.
Puntaje Z
Bajo una distribución normal, donde hay datos completos disponibles, es una distancia de la media. Su fórmula es como se da a continuación,
Z= (x-μ)/σ
Dónde,
X = datos sin procesar individuales
μ = media poblacional
σ = Desviación estándar de la población
Puntaje T
La puntuación T es la resta de la desviación estándar individual de la media individual y luego se divide el resultado con el resultado completo de la desviación estándar de la muestra multiplicado por el tamaño de la muestra. Su fórmula es como se da a continuación,
t = ((- μ)/s)*
= Media de la muestra
μ = media poblacional
s = Desviación estándar de muestra
n = tamaño de muestra
Tomemos un ejemplo para entender lo mismo de una mejor manera:
En un artículo, hay 3 subdivisiones: I, II y III. Deje que el número de estudiantes que contestaron correctamente sea del 25%, es decir, el 75% no puede responderlo correctamente. Del mismo modo, deje que el 10% y el 20% por el número de personas que respondieron las secciones II y III correctamente, por lo tanto, el 90% y el 80% han encontrado las secciones II y III. Suponemos que la capacidad medida por estos tres elementos es la misma y normalmente se distribuye,
El puntaje de cada estudiante en una clase se usa para calcular la media de las calificaciones que es igual a 50 y una desviación estándar de 10. Podemos calcular el puntaje Z con el puntaje de 50 como (50-50) / 10 = 0
Podemos interpretar que el puntaje del alumno es 0 distancia (en unidades de desviaciones estándar) de la media, por lo que el alumno obtuvo un puntaje promedio.
Si el puntaje es 60, el puntaje Z es (60-50) / 10 = 1
Podemos interpretar que el estudiante obtuvo un puntaje superior al promedio, una distancia de 1 desviación estándar por encima de la media.
Comparación cabeza a cabeza entre la puntuación Z y la puntuación T (infografía)
A continuación se muestra la diferencia de las 9 principales entre la puntuación Z y la puntuación T 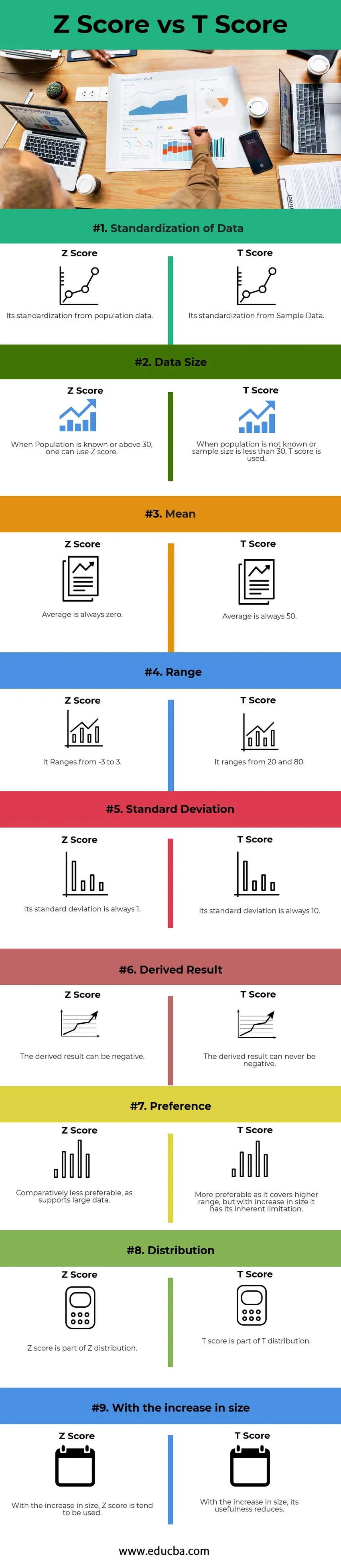
Diferencias clave entre puntaje Z vs puntaje T
Analicemos algunas de las principales diferencias entre el puntaje Z y el puntaje T
- El puntaje Z es la estandarización de los datos brutos de la población o más de 30 datos de muestra al puntaje estándar, mientras que el puntaje T es la estandarización de los datos de muestra de menos de 30 datos al puntaje estándar
- El puntaje Z varía de -3 a 3, mientras que el puntaje T varía de 20 a 80.
- A medida que aumenta el tamaño de los datos, la distribución tiende a ser distribución Z. La distribución del puntaje Z frente al puntaje T es parte de una distribución normal, pero según el tamaño difieren entre sí
- Prácticamente, el puntaje Z se usa ampliamente en los datos del mercado de valores y para verificar las posibilidades de que una empresa vaya a la quiebra, mientras que el puntaje t se usa ampliamente para verificar la densidad mineral ósea y las evaluaciones de riesgo de fractura.
Tabla comparativa de puntuación Z vs puntuación T
Veamos los 9 mejores Comparación entre puntaje Z vs puntaje T
| No Señor. | Puntos de comparación | Puntaje Z | Puntaje T |
| 1 | Estandarización de datos | Su estandarización a partir de datos de población. | Su estandarización a partir de datos de muestra |
| 2 | Tamaño de datos | Cuando la población es conocida o superior a 30, se puede usar la puntuación Z | Cuando no se conoce la población o el tamaño de la muestra es inferior a 30, se utiliza la puntuación T. |
| 3 | Media | Un promedio siempre es cero. | Un promedio es siempre 50. |
| 4 4 | Rango | Varía de -3 a 3. | Varía entre 20 y 80. |
| 5 5 | Desviación Estándar | Su desviación estándar es siempre 1 | Su desviación estándar es siempre 10 |
| 6 6 | Resultado derivado | El resultado derivado puede ser negativo. | El resultado derivado nunca puede ser negativo |
| 7 7 | Preferencia | Comparativamente menos preferible, ya que admite datos grandes | Más preferible ya que cubre un rango más alto, pero con un aumento de tamaño tiene su limitación inherente |
| 8 | Distribución | La puntuación Z es parte de la distribución Z | La puntuación T es parte de la distribución T |
| 9 9 | Con el aumento de tamaño | Con el aumento de tamaño, la puntuación Z tiende a usarse | Con el aumento de tamaño, su utilidad se reduce. |
Conclusión
Tanto el puntaje Z frente al puntaje T es parte de la prueba de hipótesis bajo la distribución normal. Si tiene un conjunto de puntajes de medición en diferentes medidas usando puntajes Z, puede decir cómo se colocan los puntajes en sus distribuciones. Entonces puedes compararlos. La estandarización de los puntajes es un procedimiento ampliamente utilizado en el campo de la investigación y la planificación, ya que ayudan en la comparación de varios puntajes de las pruebas. Estandarizar los puntajes antes de combinarlos ayuda al investigador a obtener resultados mejores y comparables.
Artículos recomendados
Esta ha sido una guía de la principal diferencia entre la puntuación Z y la puntuación T. Aquí también discutimos las diferencias clave entre la puntuación Z y la puntuación T con la infografía y la tabla de comparación. También puede echar un vistazo a los siguientes artículos para obtener más información:
- Finanzas versus economía: la mejor diferencia
- Déficit vs deuda: cuál es mejor
- Compra de activos vs compra de acciones
- Mercado monetario vs mercado de capitales
- Descripción general de Altman Z Score