
Fórmula del margen de error (tabla de contenido)
- Fórmula del margen de error
- Ejemplos de fórmula de margen de error (con plantilla de Excel)
- Calculadora de fórmula de margen de error
Fórmula del margen de error
En estadística, calculamos el intervalo de confianza para ver dónde caerá el valor de los datos de la estadística de muestra. El rango de valores que están por debajo y por encima del estadístico de muestra en un intervalo de confianza se conoce como Margen de error. En otras palabras, es básicamente el grado de error en la estadística de muestra. Cuanto mayor sea el margen de error, menor será la confianza en los resultados porque el grado de desviación en estos resultados es muy alto. Como su nombre lo indica, el margen de error es un rango de valores por encima y por debajo de los resultados reales. Por ejemplo, si recibimos una respuesta en una encuesta en la que el 70% de las personas ha respondido "bien" y el margen de error es del 5%, esto significa que, en general, del 65% al 75% de la población piensa que la respuesta es "buena" .
La fórmula para el margen de error -
Margin of Error = Z * S / √n
Dónde:
- Z - puntaje Z
- S - Desviación estándar de una población
- n - Tamaño de muestra
Otra fórmula para calcular el margen de error es:
Margin of Error = Z * √((p * (1 – p)) / n)
Dónde:
- p - Proporción de muestra (fracción de muestra que es un éxito)
Ahora, para encontrar el puntaje z deseado, debe conocer el intervalo de confianza de la muestra porque el puntaje Z depende de eso. A continuación se muestra la tabla para ver la relación de un intervalo de confianza y una puntuación z:
| Intervalo de confianza | Z - Puntuación |
| 80% | 1, 28 |
| 85% | 1, 44 |
| 90% | 1, 65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Una vez que conozca el intervalo de confianza, puede usar el valor z correspondiente y calcular el margen de error desde allí.
Ejemplos de fórmula de margen de error (con plantilla de Excel)
Tomemos un ejemplo para comprender el cálculo del Margen de error de una mejor manera.
Puede descargar esta plantilla de margen de error aquí - Plantilla de margen de errorFórmula del margen de error - Ejemplo # 1
Digamos que estamos realizando una encuesta para ver cuál es la calificación que obtienen los estudiantes universitarios. Hemos seleccionado 500 estudiantes al azar y les pedimos su calificación. El promedio de eso es 2.4 de 4 y la desviación estándar es, digamos, 30%. Suponga que el intervalo de confianza es del 99%. Calcule el margen de error.
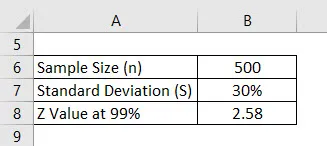
Solución:
El margen de error se calcula utilizando la fórmula que se proporciona a continuación.
Margen de error = Z * S / √n
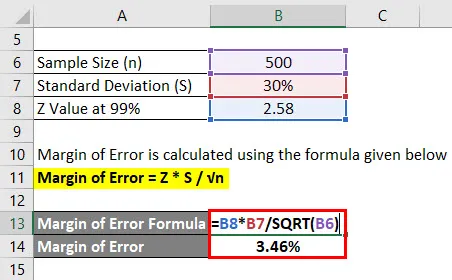
- Margen de error = 2.58 * 30% / √ (500)
- Margen de error = 3.46%
Esto significa que con un 99% de confianza, la calificación promedio de los estudiantes es 2.4 más o menos 3.46%.
Fórmula del margen de error - Ejemplo # 2
Digamos que está lanzando un nuevo producto de salud en el mercado pero está confundido sobre qué sabor le gustará a la gente. Usted está confundido entre el sabor a plátano y el sabor a vainilla y ha decidido realizar una encuesta. Su población para eso es 500, 000, que es su mercado objetivo y de eso decidió pedir la opinión de 1000 personas y esa será la muestra. Suponga que un intervalo de confianza es del 90%. Calcule el margen de error.
Solución:
Una vez que se realizó la encuesta, se dio cuenta de que a 470 personas les gustó el sabor a plátano y 530 pidieron sabor a vainilla.
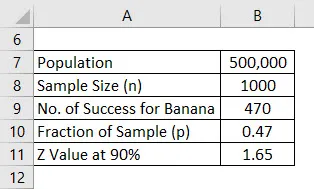
El margen de error se calcula utilizando la fórmula que se proporciona a continuación.
Margen de error = Z * √ ((p * (1 - p)) / n)
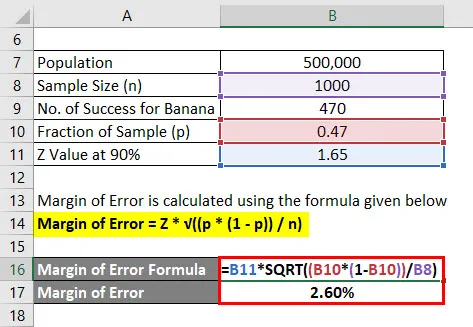
- Margen de error = 1.65 * √ ((0.47 * (1 - 0.47)) / 1000)
- Margen de error = 2.60%
Entonces, podemos decir que con un 90% de confianza de que al 47% de todas las personas les gustó el sabor de plátano más o menos 2.60%.
Explicación
Como se discutió anteriormente, el margen de error nos ayuda a comprender si el tamaño de la muestra de su encuesta es apropiado o no. En caso de que el error de margen sea demasiado grande, puede ser el caso de que nuestro tamaño de muestra sea demasiado pequeño y necesitemos aumentarlo para que los resultados de la muestra coincidan más estrechamente con los resultados de la población.
Hay algunos escenarios en los que el margen de error no será de mucha utilidad y no nos ayudará a rastrear el error:
- Si las preguntas de la encuesta no están diseñadas y no ayudan a obtener la respuesta requerida
- Si las personas que responden a la encuesta tienen algún sesgo con respecto al producto para el que se realiza la encuesta, entonces, el resultado no será muy preciso
- Si la muestra elegida en sí misma es el representante adecuado de la población, en ese caso también, los resultados estarán muy lejos.
Además, una gran suposición aquí es que la población está normalmente distribuida. Entonces, si el tamaño de la muestra es demasiado pequeño y la distribución de la población no es normal, no se puede calcular el puntaje z y no podremos encontrar el margen de error.
Relevancia y usos de la fórmula del margen de error
Cada vez que usamos datos de muestra para encontrar alguna respuesta relevante para el conjunto de la población, existe cierta incertidumbre y posibilidades de que el resultado pueda desviarse del resultado real. El margen de error nos dirá que cuál es el nivel de desviación si existe la salida de muestra. Necesitamos minimizar el margen de error para que nuestros resultados de muestra muestren la historia real de los datos de población. Entonces, reduzca el margen de error, mejores serán los resultados. El margen de error complementa y completa la información estadística que tenemos. Por ejemplo, si una encuesta determina que el 48% de las personas prefieren pasar tiempo en casa durante el fin de semana, no podemos ser tan precisos y hay algunos elementos que faltan en esa información. Cuando introdujimos un margen de error aquí, digamos, 5%, entonces el resultado se interpretará como 43-53% de las personas les gustó la idea de estar en casa durante el fin de semana, lo que tiene mucho sentido.
Calculadora de fórmula de margen de error
Puede usar la siguiente calculadora de margen de error
| Z | |
| S | |
| √n | |
| Margen de error | |
| Margen de error | = |
|
|
Artículos recomendados
Esta ha sido una guía para la fórmula Margen de error. Aquí discutimos cómo calcular el Margen de error junto con ejemplos prácticos. También proporcionamos una calculadora de margen de error con plantilla de Excel descargable. También puede consultar los siguientes artículos para obtener más información:
- Guía para la fórmula de depreciación en línea recta
- Ejemplos de fórmula de tiempo de duplicación
- ¿Cómo calcular la amortización?
- Fórmula para el teorema del límite central
- Puntuación Altman Z | Definición | Ejemplos
- Fórmula de amortización | Ejemplos con plantilla de Excel