
Fórmula Z Score (Tabla de contenido)
- Fórmula
- Ejemplos
- Calculadora
¿Qué es la fórmula Z Score?
El "puntaje Z" es una de las herramientas estadísticas más utilizadas que se utiliza para estandarizar el puntaje, siempre y cuando se conozca la población y la desviación estándar. Como tal, el puntaje Z también se conoce como puntaje estándar. La puntuación Z varía en el rango de -3 veces la desviación estándar a +3 veces la desviación estándar con una media de cero y una desviación estándar de uno. La fórmula para el puntaje Z de una variable se puede deducir deduciendo la media de la población de la variable dada (que es parte del conjunto de datos o población) y luego dividiendo el resultado por la desviación estándar de la población. Matemáticamente, se representa como,
Z = (X – μ) / σ
dónde,
- X = variable de la población
- μ = media de la población
- σ = Desviación estándar de la población
Ejemplos de fórmula de puntuación Z (con plantilla de Excel)
Tomemos un ejemplo para comprender el cálculo de la puntuación Z de una mejor manera.
Puede descargar esta plantilla Excel de Z Score Formula aquí - Plantilla Excel de Z Score FormulaFórmula Z Score - Ejemplo # 1
Tomemos el ejemplo de Manny que apareció recientemente para SAT. Logró anotar 1109 en este intento. Sin embargo, según la información disponible, el puntaje promedio para SAT permaneció alrededor de 1030 con una desviación estándar de 250. Calcule el puntaje Z para el puntaje SAT de Manny y evalúe qué tan bien lo hizo en comparación con los examinados promedio.
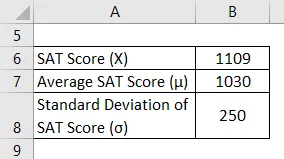
Solución:
La puntuación Z se calcula utilizando la fórmula que se proporciona a continuación
Z = (X - μ) / σ
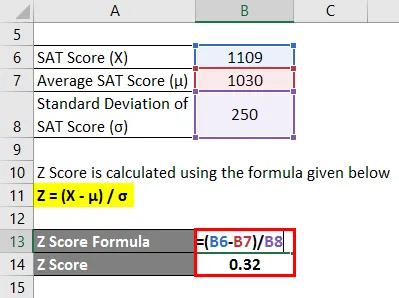
- Puntaje Z = (1109-1030) / 250
- Puntaje Z = 0.32
Por lo tanto, el puntaje SAT de Manny es 0.32 desviación estándar más alta que el puntaje promedio de los examinados, lo que indica que el 62.55% de los examinados obtuvo un puntaje menor que Manny.
Fórmula Z Score - Ejemplo # 2
Ahora, tomemos el ejemplo de Chelsea, que ha escrito el SAT dos veces y quiere comparar su desempeño en ellos. Se las arregló para anotar 1085 y 1059 en sus 1.º y 2.º intentos respectivamente. Según la información disponible, el puntaje promedio y la desviación estándar durante el primer intento fueron 1100 y 230 respectivamente, mientras que en el último fue 1050 y 240 respectivamente. Ayude a Chelsea a decidir en qué examen se desempeñó mejor.
Solución:
1er intento
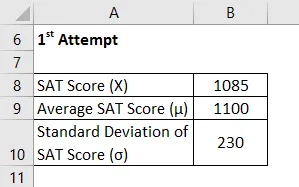
La puntuación Z se calcula utilizando la fórmula que se proporciona a continuación
Z = (X - μ) / σ
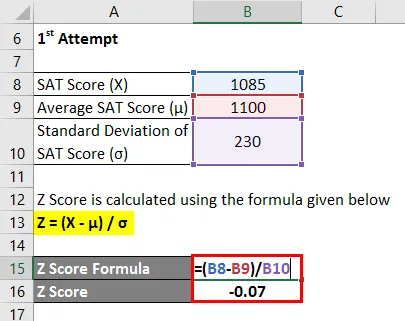
- Puntaje Z = (1085-1100) / 230
- Puntaje Z = -0.07
Por lo tanto, el puntaje SAT del Chelsea en el primer intento es 0.07 desviación estándar más baja que el puntaje promedio de los examinados, lo que indica que el 47.40% de los examinados obtuvo menos puntaje que el Chelsea durante el primer intento.
2º intento
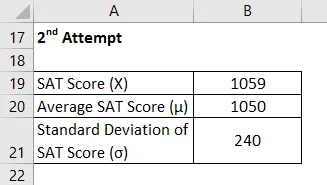
La puntuación Z se calcula utilizando la fórmula que se proporciona a continuación
Z = (X - μ) / σ
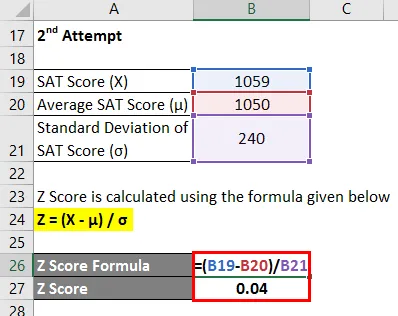
- Puntaje Z = (1059-1050) / 240
- Puntaje Z = 0.04
Por lo tanto, el puntaje SAT del Chelsea en el segundo intento es 0.04 desviación estándar más alta que el puntaje promedio de los examinados, lo que indica que el 51.50% de los examinados obtuvo menos puntaje que el Chelsea durante el segundo intento.
Entonces, a partir de la comparación de los puntajes Z, está claro que Chelsea tuvo un mejor desempeño durante su segundo intento.
Explicación
La fórmula para la puntuación Z se puede derivar mediante los siguientes pasos:
Paso 1: Primero, construya una población con una gran cantidad de variables y las variables se denotan por X i .
Paso 2: A continuación, se calcula el número de variables en la población y se denota por N.
Paso 3: A continuación, la media de la población se calcula sumando todas las variables seguidas de la división por el número total de variables (paso 2) en el conjunto de datos. La media de la población se denota por μ.
μ = ∑ X i / N
Paso 4: Luego, deduzca la media de cada variable del conjunto de datos para calcular su desviación de la media.
es decir (X i - μ) es la desviación para el iésimo punto de datos.
Paso 5: A continuación, calcule las desviaciones al cuadrado de las variables, es decir (X i - μ) 2 .
Paso 6: Luego, sume todas las desviaciones al cuadrado y luego divida el total por el número de variables en el conjunto de datos para llegar a la varianza.
σ 2 = ∑ (X i - μ) 2 / N
Paso 7: A continuación, la desviación estándar de la población se calcula calculando la raíz cuadrada de la varianza calculada en el paso anterior.
σ = √ ∑ (X i - μ) 2 / N
Paso 8: Finalmente, la fórmula para el puntaje Z se obtiene deduciendo la media de la población (paso 3) de la variable y luego dividiendo el resultado por la desviación estándar de la población (paso 7) como se muestra a continuación.
Z = (X - μ) / σ
Relevancia y usos de la fórmula Z Score
Desde la perspectiva de un estadístico, el concepto de puntaje Z es muy importante ya que es útil para determinar la probabilidad de que ocurra o no un evento dentro de una distribución normal. De hecho, el puntaje Z también se usa para comparar dos puntajes brutos de dos distribuciones normales diferentes y se realiza convirtiendo los puntajes brutos en puntaje Z o puntaje estandarizado. Además, una puntuación Z positiva implica una puntuación más alta que la media, mientras que una puntuación Z negativa implica una puntuación menor que la media.
Calculadora de fórmula de puntaje Z
Puede usar la siguiente calculadora de fórmula de puntaje Z
| X | |
| µ | |
| σ | |
| Z | |
| Z = |
|
|
Artículos recomendados
Esta ha sido una guía para la fórmula Z Score. Aquí discutimos cómo calcular la puntuación Z junto con ejemplos prácticos. También proporcionamos una calculadora Z Score con plantilla de Excel descargable. También puede consultar los siguientes artículos para obtener más información:
- Ejemplos de fórmula de tamaño de muestra
- ¿Cómo calcular la media ponderada?
- Calculadora para fórmula de correlación
- Fórmula para calcular la distribución normal
- Ejemplos de Altman Z Score