Números complejos en MATLAB - ¿Cómo generar un número complejo?

Introducción a los números complejos en MATLAB

Los números complejos son la combinación de números reales y números imaginarios en forma de p + qi donde p y q son los números reales e i es el número imaginario. Se define un número imaginario donde i es el resultado de una ecuación a 2 = -1. Podemos usar i o j para denotar las unidades imaginarias. Como los números complejos se usan en cualquier cálculo matemático y Matlab se usa principalmente para realizar cálculos matemáticos. Entonces, los números complejos forman una parte importante del aprendizaje de Matlab.

Generación de números complejos en MATLAB

Los números complejos se pueden crear o declarar en Matlab usando una función 'compleja'. También podemos crear números complejos al encontrar la raíz cuadrada de cualquier número negativo. En Matlab, podemos usar i o j para denotar la parte imaginaria del número complejo.

Ejemplos

X = 4 + 5i

Aquí X es un número complejo que contiene 2 partes, es decir, parte real e imaginaria. 4 es la parte real y 5 es la parte imaginaria. Podemos encontrar las partes reales e imaginarias usando funciones en Matlab.

a = real (X) = 4 (Esto da la parte real del número complejo)
b = imag (X) = 5 (Esto da la parte imaginaria del número complejo)
complejo (6, 7) = 6 + 7i (esta función se utiliza para crear un número complejo)

También podemos crear matrices complejas en Matlab que también se pueden declarar utilizando las funciones complejas.

a = complejo (x, y)

Hay ciertas condiciones para x e y que debemos seguir, como x e y no deben ser simples o dobles. Se puede crear un escalar complejo si dos entradas son de naturaleza escalar como,

X = complejo (5, 3)
X = 5.0000 + 3.0000i

Del mismo modo, se puede crear un vector complejo si tenemos dos entradas como vectores.

X = uint8 ((4; 5; 6; 7));
Y = uint8 ((3; 5; 1; 2));
a = complejo (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Podemos crear un número complejo que tenga un solo escalar como,

X = complejo (10)
X = 10.0000 + 0.0000i

Hay ciertas condiciones que los argumentos de entrada y salida deben seguir, como

Los argumentos de entrada contienen partes reales e imaginarias como x any y. xey deben ser escalares, vectoriales, matriz multidimensional o matriz en MATLAB. El tamaño xey debe ser el mismo. Deben ser del mismo tipo de datos, pero hay algunas excepciones, como el doble se puede usar con un solo y el entero se puede combinar con un doble que es escalar.

La salida de la matriz puede ser vectorial, escalar, matriz o matriz multidimensional dependiendo de los argumentos de entrada. El tamaño de la salida debe ser el mismo que el de la entrada. Si los argumentos de entrada son de tipos de datos diferentes a los que determina la salida,

Si cualquiera de los argumentos de entrada es de naturaleza única, la salida también debería ser única.
Si cualquiera de los argumentos de entrada es de naturaleza entera, entonces la salida debe ser de un tipo de datos entero.

Podemos verificar si la matriz es real o imaginaria usando la función isreal.

Código:

X = (2+i, 1); Isreal(X)

Salida:

Código:

Isreal (X (2))

Salida:

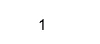
Para extraer las partes reales e imaginarias, podemos usar funciones reales e imag en Matlab como,

Código:

real(X)

Salida:

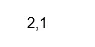
Código:

imag(X)

Salida:

Operaciones y funciones de números complejos en MATLAB

Hay varias operaciones y funciones que se pueden realizar usando números complejos en Matlab como

abs: esta función se utiliza para encontrar el módulo de cualquier número complejo en forma de p + qi. abs (2 + 3i) = raíz cuadrada de (2 2 + 3 2) = (13) 0.5
ángulo: para encontrar el ángulo de fase del número complejo.

Hay ciertos consejos que deben seguirse para el correcto funcionamiento de números complejos en Matlab como,

Deberíamos evitar usar i y j como parte de cualquier nombre de variable, ya que se usan para denotar las partes imaginarias del número complejo.
Deberíamos evitar usar j o i si la parte imaginaria es 1. En su lugar, podemos usar 1j o 1i.
Podemos crear una función compleja en Matlab cuando i y j se usan como nombres de variables en alguna parte, los argumentos de entrada no son de tipo simple o doble y la parte imaginaria es cero.

Conclusión

Los números complejos se usan en el campo matemático o de ingeniería. Muchas aplicaciones prácticas o de la vida real pueden describirse utilizando la parte imaginaria de números complejos. Por lo tanto, comprender el uso y las aplicaciones de los números complejos en varias plataformas es importante, especialmente si se trata de un dominio físico o matemático.

Artículos recomendados

Esta es una guía de números complejos en MATLAB. Aquí discutimos la introducción y la generación de números complejos en matlab, incluidos sus ejemplos con operación y función. También puede consultar los siguientes artículos para obtener más información.