
Introducción a las funciones en R
La función se define como un conjunto de declaraciones, para realizar y realizar cualquier tarea lógica específica. La función toma algunos parámetros de entrada que se conocen como argumentos para realizar esa tarea. Las funciones ayudan a dividir el código, en trozos más simples al orquestarlo lógicamente, lo que es más fácil de leer y comprender. En este tema, vamos a aprender sobre Funciones en R.
¿Cómo escribir funciones en R?
Para escribir la función en R, aquí está la sintaxis:
Fun_name <- function (argument) (
Function body
)
Aquí, uno puede ver que la palabra reservada específica de "función" se usa en R, para definir cualquier función. La función toma la entrada en forma de argumentos. El cuerpo de la función es un conjunto de declaraciones lógicas que se realizan sobre argumentos y luego devuelve el resultado. "Fun_name" es el nombre dado a la función, a través del cual se puede invocar en cualquier parte del programa R.
Veamos un ejemplo, que será más lúcido en la comprensión del concepto de función en R.
Código R
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
salida:
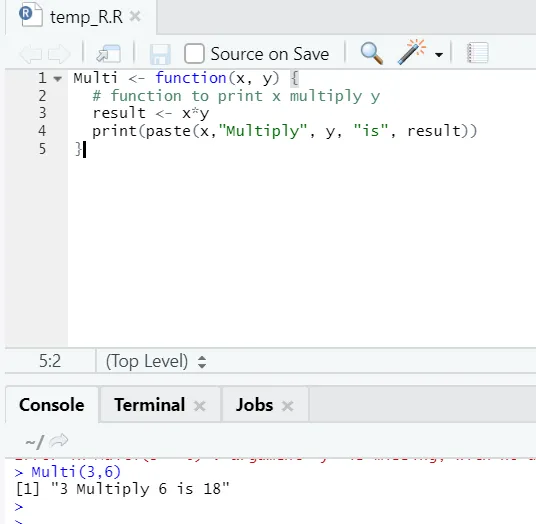
Aquí creamos el nombre de la función "Multi", que toma dos argumentos como entradas y proporciona la salida multiplicada. El primer argumento es xy el segundo argumento es y. Como puede ver, hemos llamado a la función por el nombre "Multi". Aquí, si alguien quiere, los argumentos también se pueden establecer en el valor predeterminado.
Diferentes tipos de funciones en R
Diferentes funciones R con sintaxis y ejemplos (incorporado, matemático, estadístico, etc.)
1) Función incorporada -
Estas son las funciones que vienen con R para abordar una tarea específica tomando un argumento como entrada y dando una salida basada en la entrada dada. Analicemos algunas funciones generales importantes de R aquí:
a) Ordenar: los datos pueden ser del orden ascendente o descendente. Los datos pueden ser si un vector de variable continua o variable de factor.
Sintaxis:

Aquí está la explicación de sus parámetros:
- x: Este es un vector de la variable continua o variable de factor
- decreciente: Esto se puede configurar como Verdadero / Falso para controlar el orden ascendente o descendente. Por defecto, es FALSO`.
- último: si el vector tiene valores de NA, debe colocarse al final o no
Código R y salida:
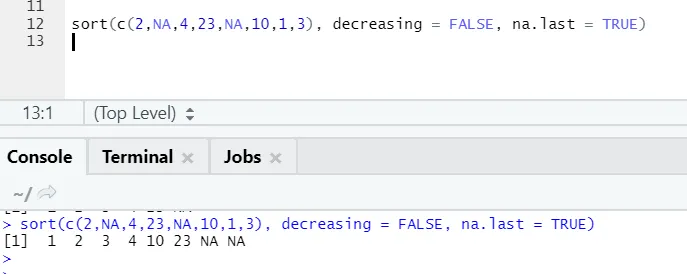
Aquí se puede observar cómo los valores "NA" se alinean al final. Como nuestro parámetro na.last = True era verdadero.
b) Seq: genera una secuencia del número entre dos números especificados.
Sintaxis
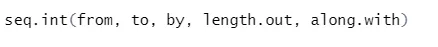
Aquí está la explicación de sus parámetros:
- desde, hasta el valor inicial y final de la secuencia.
- por: Incremento / brecha entre dos números consecutivos en secuencia
- length.out: la longitud requerida de la secuencia.
- Along.with: se refiere a la longitud de la longitud de este argumento
Código R y salida:
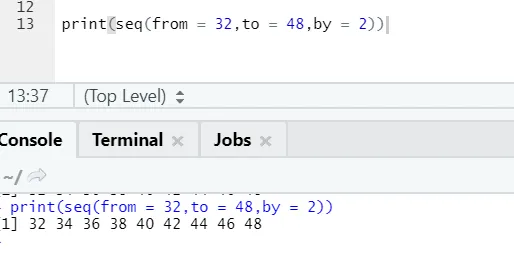
Aquí se puede notar que la secuencia generada tiene un incremento de 2 porque by se define como 2.
c) Toupper, tolower: las dos funciones: toupper y tolower son funciones que se aplican en la cadena para cambiar los casos de las letras en las oraciones.
Código R y salida:
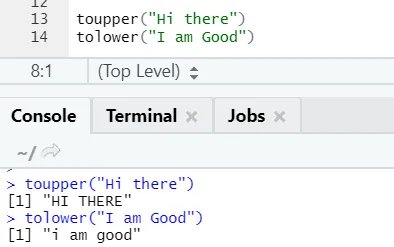
Uno puede notar cómo cambian los casos de letras cuando se aplican a la función.
d) Rnorm: esta es una función incorporada que genera números aleatorios.
Código R y salida:
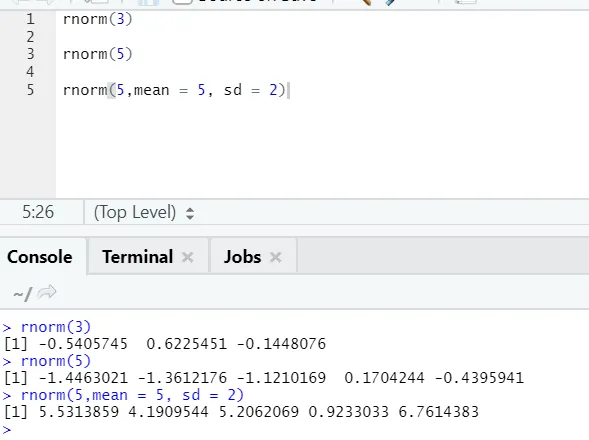
La función rnorm toma el primer argumento que dice cuántos números deben generarse.
e) Rep: Esta función replica el valor tantas veces como se especifica.
Sintaxis R: rnorm (x, n)
Aquí x representa el valor para replicar, yn representa el número de veces que tiene que replicarse.
Código R y salida:
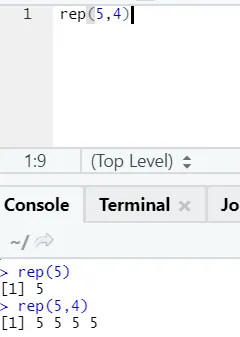
f) Pegar: esta función es para concatenar cadenas junto con algún carácter específico en el medio.
sintaxis
paste(x, sep = “”, collapse = NULL)
Código R
paste("fish", "water", sep=" - ")
Salida R:
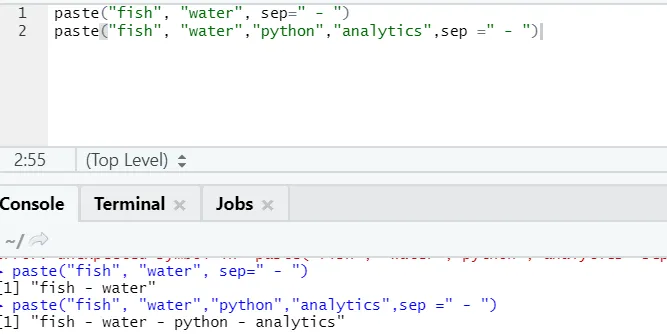
Como puede ver, también podemos pegar más de dos cadenas. Sep es ese carácter específico que agregamos entre cadenas. Por defecto, sep es espacio.
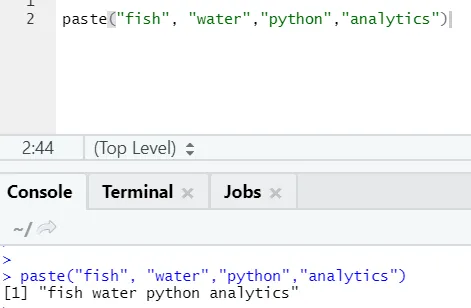
Existe una función similar más como esta, que todos deberían tener en cuenta es paste0.
La función paste0 (x, y, collapse) funciona de manera similar a paste (x, y, sep = “”, collapse)
Por favor vea el siguiente ejemplo:
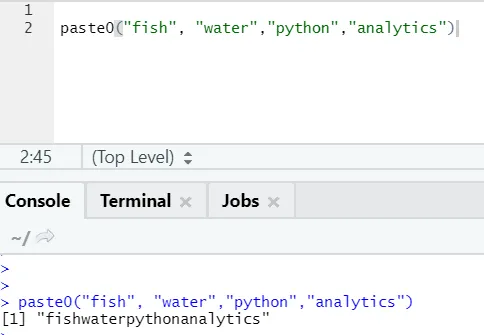
En palabras simples, para resumir pegar y pegar0:
Paste0 es más rápido que pegar cuando se trata de la concatenación de cadenas sin ningún separador. Como pegar siempre busca "sep" y que es espacio por defecto en él.
g) Strsplit: esta función es dividir la cadena. Veamos los casos simples:
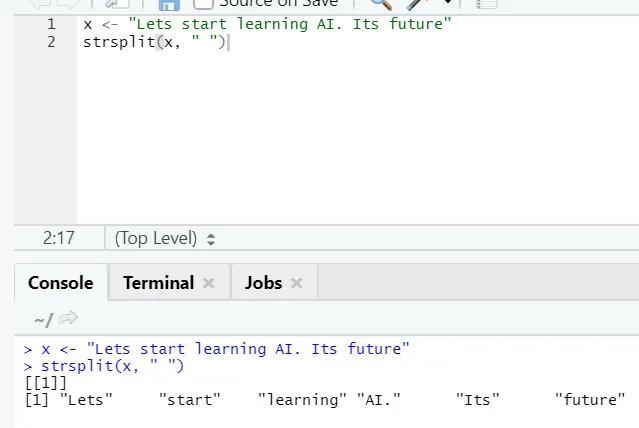
h) Rbind: la función rbind ayuda a peinar vectores con el mismo número de columnas, una sobre otra.
Ejemplo
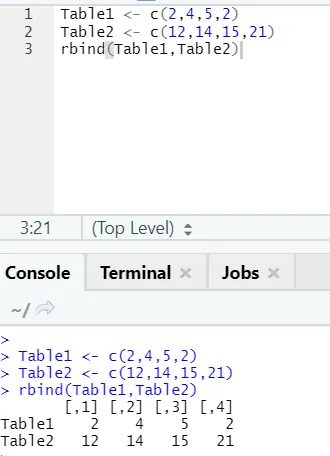
i) cbind: combina vectores con el mismo número de filas, una al lado de la otra.
Ejemplo
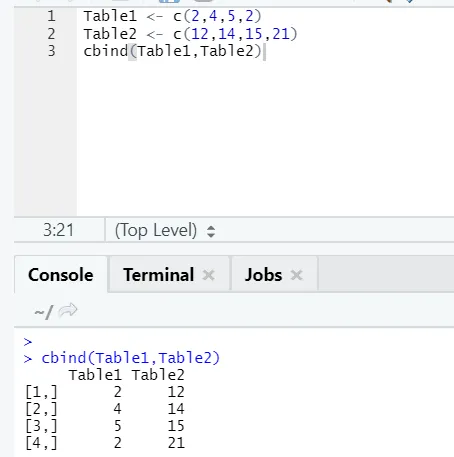
En caso de que el número de filas no coincida, a continuación se encuentra el error que encontrará:

Tanto cbind como rbind ayudan en la manipulación y remodelación de datos.
2) Función matemática -
R proporciona una amplia variedad de funciones matemáticas. Veamos algunos de ellos en detalle:
a) Sqrt: esta función calcula la raíz cuadrada de un número o vector numérico.
Código R y salida:
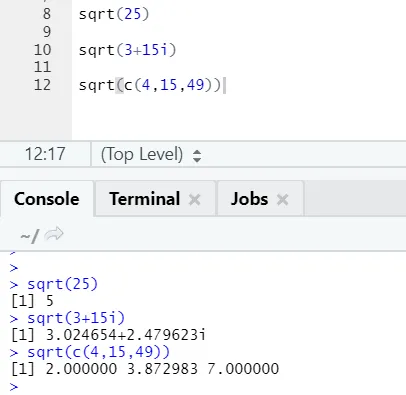
Se puede ver cómo se ha calculado la raíz cuadrada de un número, un número complejo y una secuencia de vector numérico.
b) Exp: Esta función calcula el valor exponencial de un número o un vector numérico.
Código R y salida:
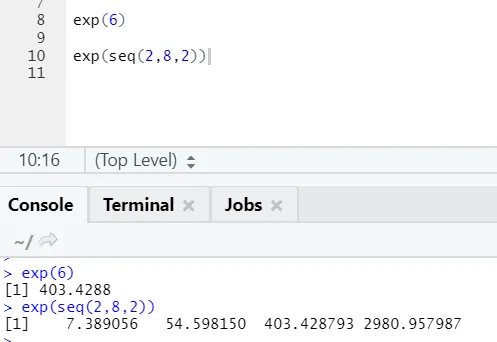
c) Cos, Sin, Tan: Estas son funciones de trigonometría implementadas en R aquí.
Código R y salida:
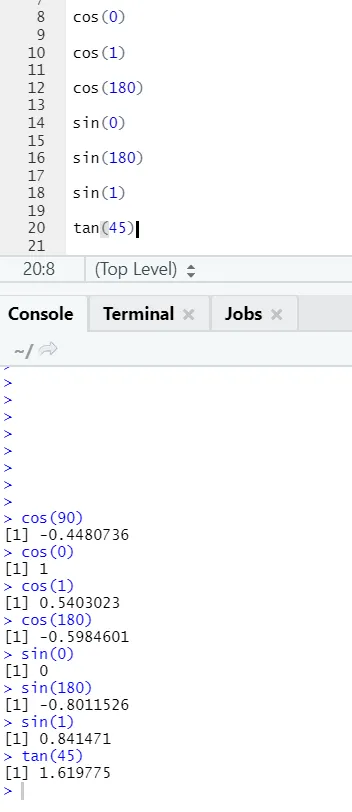
d) Abs: esta función devuelve el valor positivo absoluto de un número.
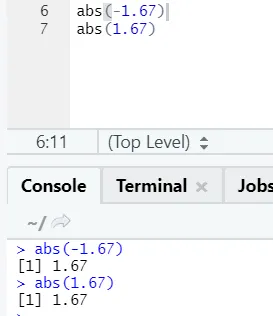
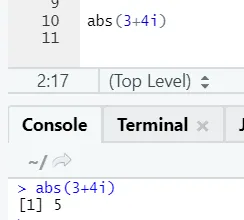
Como puede ver, lo negativo o positivo de un número se devolverá en su forma absoluta. Vamos a verlo para un número complejo:
e) Registro: Esto es para encontrar el logaritmo de un número.
Aquí está el ejemplo que se muestra a continuación:
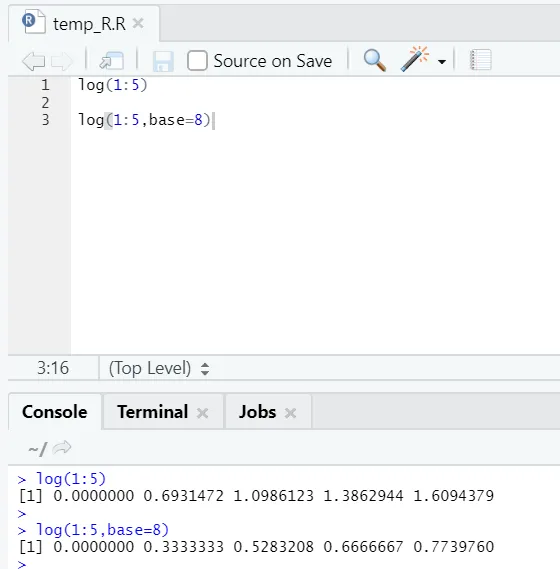
Aquí se obtiene la flexibilidad para cambiar la base, según los requisitos.
f) Cumsum: esta es una función matemática que da sumas acumulativas. Aquí está el ejemplo a continuación:
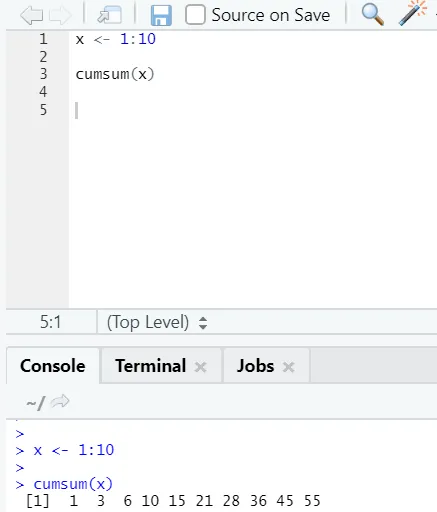
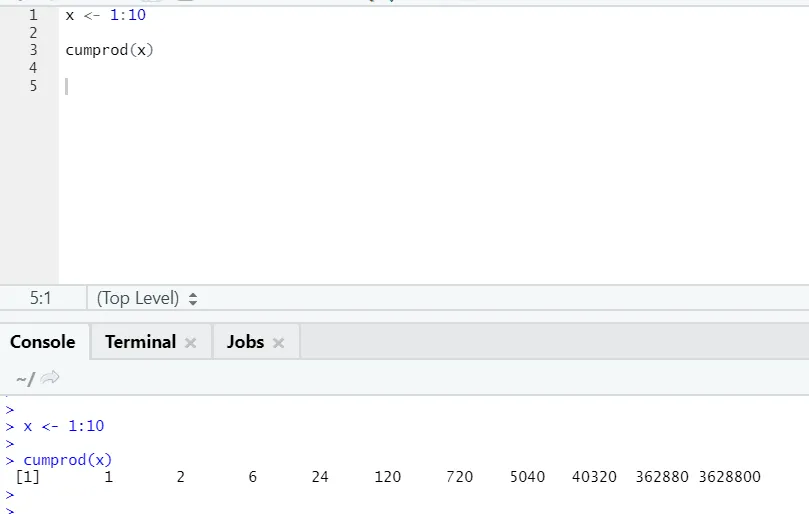
g) Cumprod: Al igual que la función matemática de Cumsum, tenemos cumprod donde ocurre la multiplicación acumulativa.
Por favor vea el siguiente ejemplo:
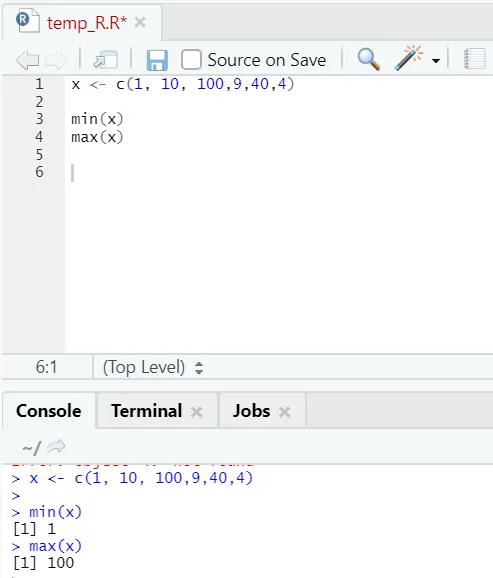
h) Máx., Mín .: esto le ayudará a encontrar el valor máximo / mínimo en el conjunto de números. Vea a continuación los ejemplos relacionados con esto:
i) Techo: el techo es una función matemática que devuelve el menor de los enteros más alto que el especificado.
Deje mira un ejemplo:
techo (2, 67)
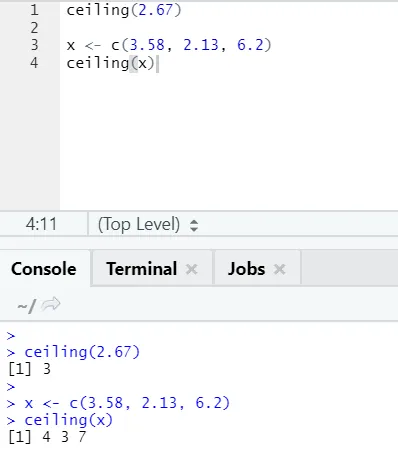
Como puede observar, el límite máximo se aplica sobre un número y sobre una lista, y el resultado es el más pequeño del siguiente entero más alto.
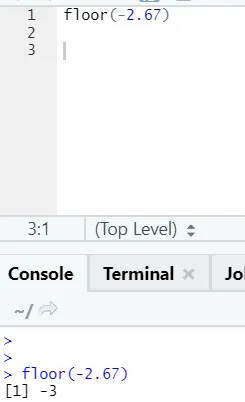
j) Piso: el piso es una función matemática que devuelve el entero de menor valor del número especificado.
El ejemplo que se muestra a continuación lo ayudará a comprenderlo mejor:
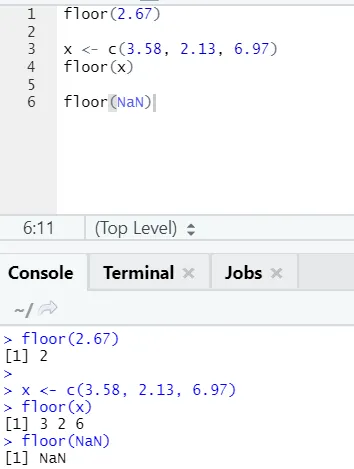
Funciona de la misma manera para valores negativos también. Por favor echa un vistazo:
3) Funciones estadísticas -
Estas son las funciones que describen la distribución de probabilidad relacionada.
a) Mediana: Esto calculó la mediana a partir de la secuencia de números.
Sintaxis
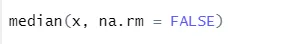
Código R y salida:
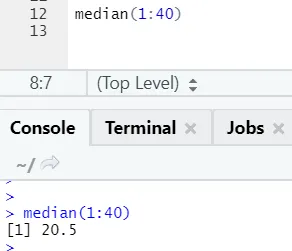
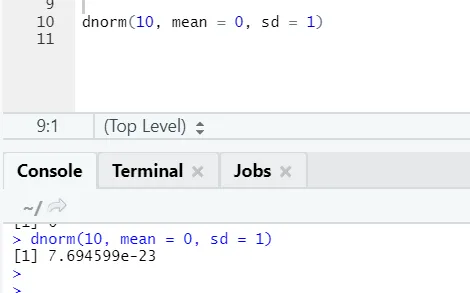
b) Dnorm: se refiere a la distribución normal. La función dnorm devuelve el valor de la función de densidad de probabilidad para los parámetros dados de distribución normal para x, μ y σ.
Código R y salida:
c) Cov: la covarianza indica si dos vectores están positiva, negativa o totalmente no relacionados.
Código R
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
Salida R:
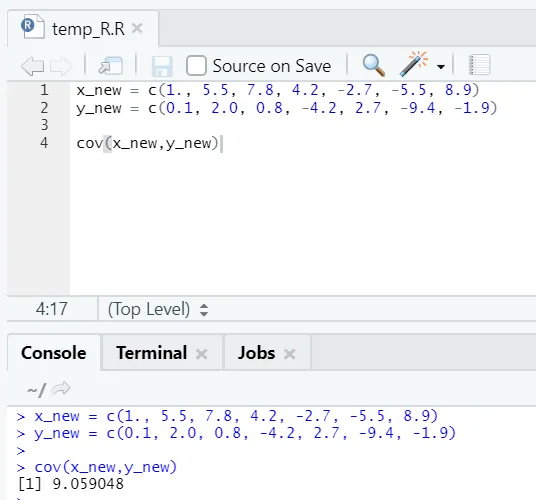
Como puede ver, dos vectores están relacionados positivamente, lo que significa que ambos vectores se mueven en la misma dirección. Si la covarianza es negativa, significa que xey están inversamente relacionadas y, por lo tanto, se mueve en la dirección opuesta.
d) Cor: Esta es una función para encontrar la correlación entre vectores. Realmente da el factor de asociación entre los dos vectores que se conoce como el "coeficiente de correlación". La correlación agrega un factor de grado sobre la covarianza. Si dos vectores están correlacionados positivamente, la correlación también le dirá con qué extensión están relacionados positivamente.
Estos tres tipos de métodos se pueden usar para encontrar una correlación entre dos vectores:
- Correlación de Pearson
- Correlación de Kendall
- Correlación de Spearman
En formato R simple, se ve así:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Aquí x e y son vectores.
Veamos el ejemplo práctico de correlación sobre un conjunto de datos incorporado.
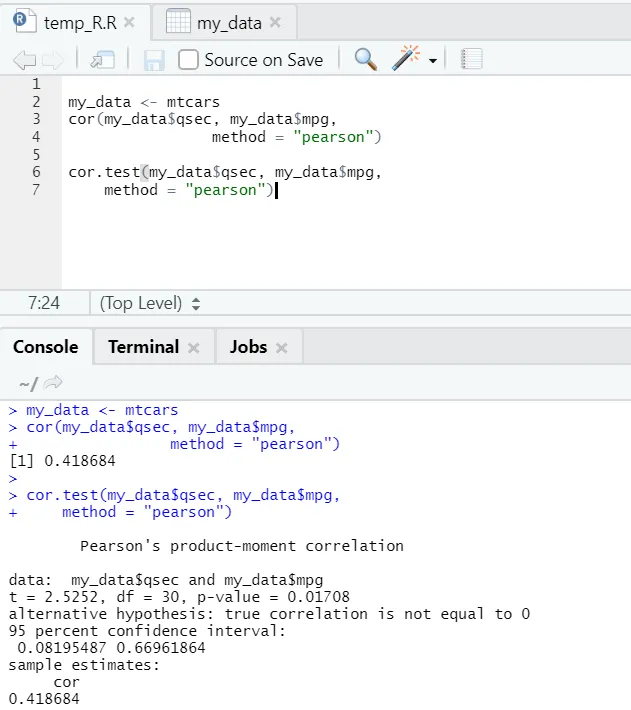
Entonces, aquí puede ver que la función "cor ()" dio el coeficiente de correlación 0.41 entre "qsec" y "mpg". Sin embargo, también se ha mostrado una función más, es decir, "cor.test ()", que no solo indica el coeficiente de correlación sino también el valor p y el valor t relacionados con él. La interpretación se vuelve mucho más fácil con la función cor.test.
Se puede hacer algo similar con los otros dos métodos de correlación:
Código R para el método Pearson:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
Código R para el método Kendall:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
Código R para el método Spearman:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
El coeficiente de correlación oscila entre -1 y 1.
Si el coeficiente de correlación es negativo, eso implica que cuando x aumenta y disminuye.
Si el coeficiente de correlación es cero, eso implica que no existe asociación entre x e y.
Si el coeficiente de correlación es positivo, eso implica que cuando x aumenta y también tiende a aumentar.
e) Prueba T: La prueba T le dirá si dos conjuntos de datos provienen de la misma (suponiendo) distribuciones normales o no.
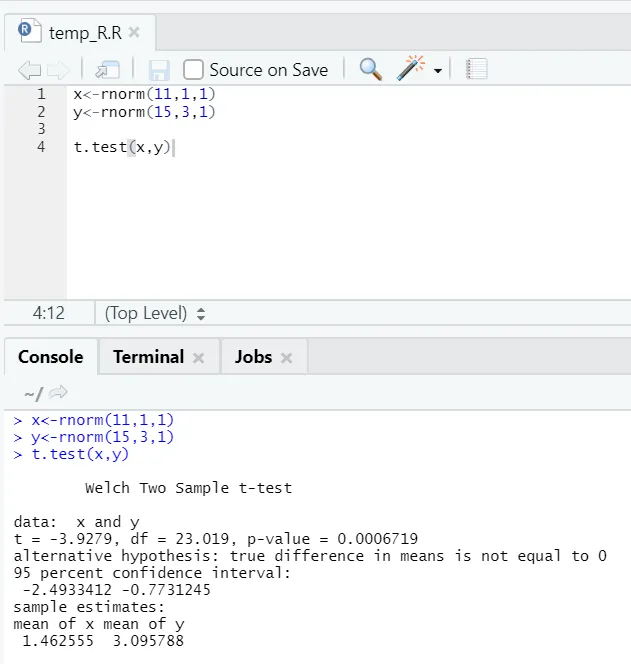
Aquí debe rechazar la hipótesis nula de que las dos medias son iguales porque el valor p es menor que 0.05.
Esta instancia que se muestra es de tipo: conjuntos de datos no apareados con variaciones desiguales. Del mismo modo, se puede probar con el conjunto de datos emparejado.
f) Regresión lineal simple: muestra la relación entre el predictor / independiente y la respuesta / variable dependiente.
Un ejemplo práctico simple podría ser predecir el peso de una persona si se conoce la altura.
Sintaxis R
lm(formula, data)
Aquí la fórmula representa la relación entre la salida, es decir, y la variable de entrada, iex. Los datos representan el conjunto de datos, en el que la fórmula debe aplicarse.
Veamos un ejemplo práctico, donde el área de piso es la variable de entrada y rent es la variable de salida.
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
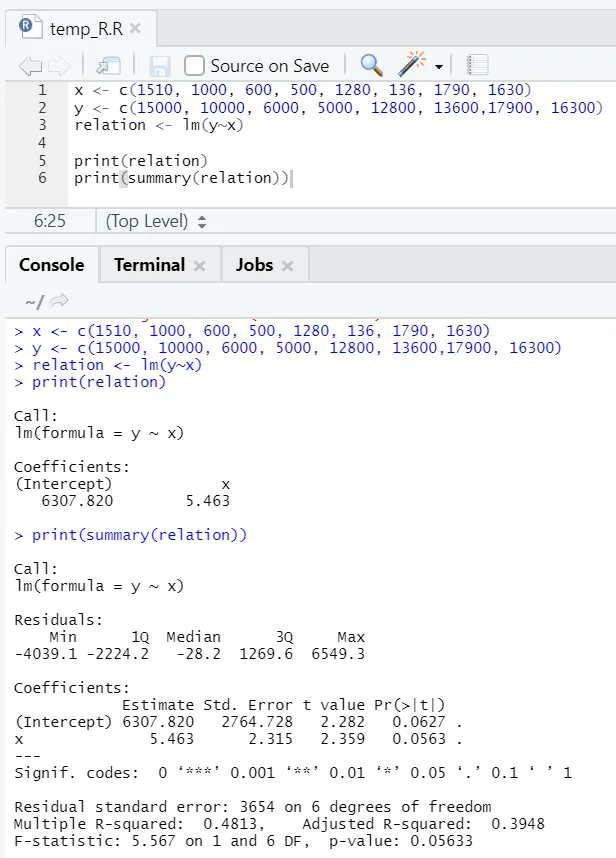
Aquí el valor P no es inferior al 5%. Por lo tanto, la hipótesis nula no puede ser rechazada. No hay mucha importancia para probar la relación entre el área del piso y el alquiler.
Aquí el valor R cuadrado es 0.4813. Eso implica que solo el 48% de la varianza en la variable de salida puede explicarse por la variable de entrada.
Digamos ahora que necesitamos predecir un valor de área de piso, basado en el modelo ajustado anteriormente.
Código R
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
Salida R:
Después de la ejecución del código R anterior, la salida tendrá el siguiente aspecto:
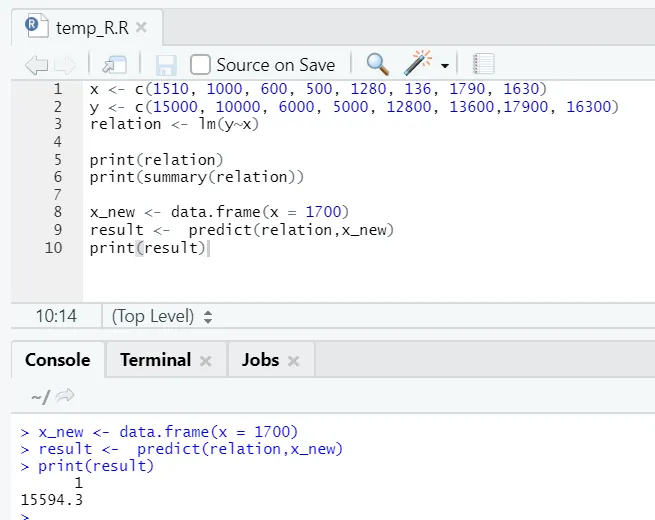
Uno puede encajar y visualizar la regresión. Aquí está el código R para eso:
# Asigne un nombre al archivo de gráfico png.
png(file = "LinearRegressionSample.png.webp")
# Trazar el gráfico.
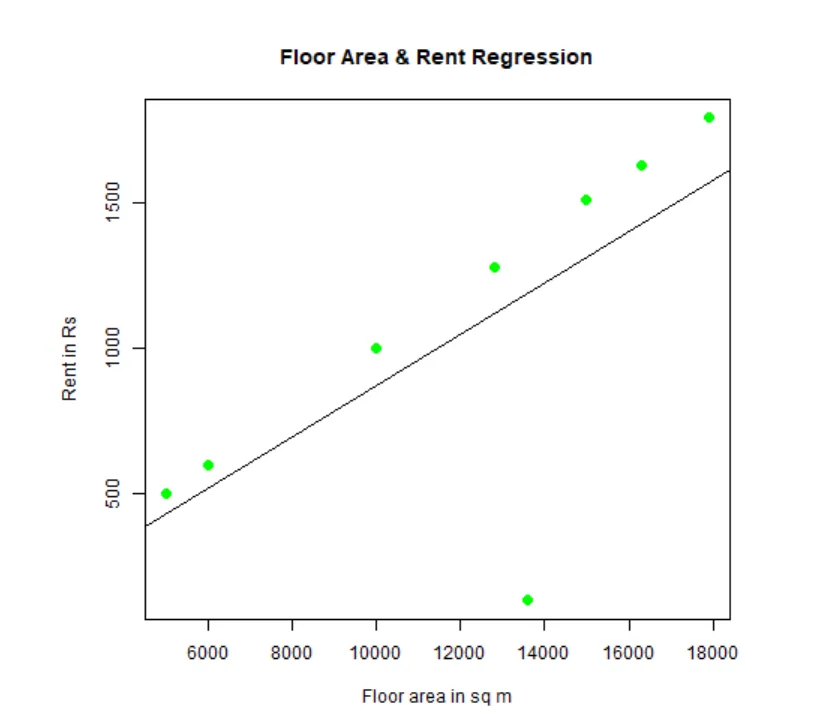
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Guarda el archivo.
dev.off()
Este gráfico "LinearRegressionSample.png.webp" se generará en su directorio de trabajo actual.
g) Prueba de Chi-cuadrado
Esta es una función estadística en R. Esta prueba tiene su importancia para demostrar si existe la correlación entre dos variables categóricas.
Esta prueba también funciona como cualquier otra prueba estadística basada en el valor p, se puede aceptar o rechazar la hipótesis nula.
Sintaxis R
chisq.test(data), /code>
Veamos un ejemplo práctico de ello.
Código R
# Cargue la biblioteca.
library(datasets)
data(iris)
# Crear un marco de datos a partir del conjunto de datos principal.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Crear una tabla con las variables necesarias.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Realice la prueba Chi-Square.
print(chisq.test(iris.data))
Salida R:
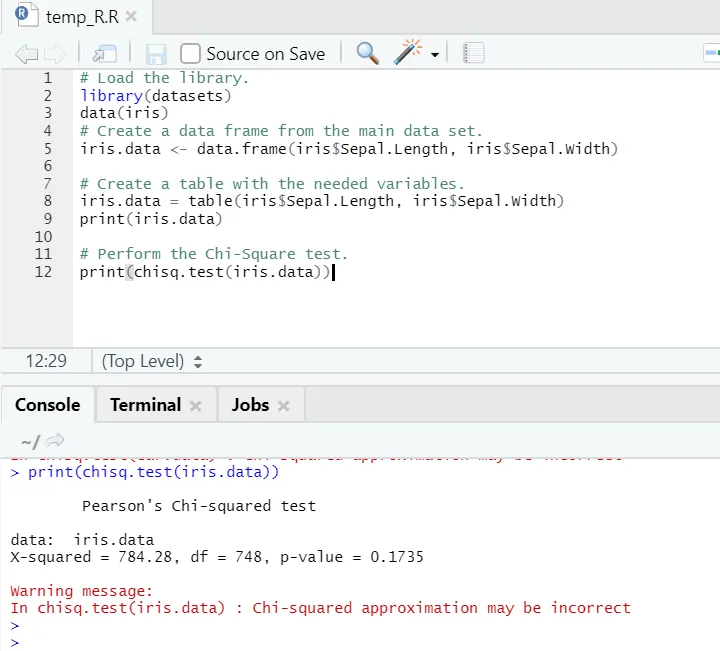
Como se puede ver, la prueba de chi-cuadrado se realizó sobre un conjunto de datos de iris, considerando sus dos variables “Sepal. Longitud "y" Sepal.Width ".
El valor p no es menor que 0.05, por lo tanto, no existe correlación entre estas dos variables. O podemos decir que estas dos variables no son dependientes entre sí.
Conclusión
Las funciones en R son simples, fáciles de ajustar, fáciles de entender y muy potentes. Vimos una variedad de funciones que se usan como parte de los conceptos básicos en R. Una vez que uno se sienta cómodo con estas funciones discutidas anteriormente, puede explorar otras variedades de funciones. Las funciones lo ayudan a hacer que su código se ejecute de manera simple y concisa. Las funciones pueden estar incorporadas o definidas por el usuario, todo depende de la necesidad al abordar un problema. Las funciones dan buena forma a un programa.
Artículos recomendados
Esta es una guía de Funciones en R. Aquí discutimos cómo escribir Funciones en R y diferentes tipos de Funciones en R con sintaxis y ejemplos. También puede consultar el siguiente artículo para obtener más información:
- Funciones de cadena R
- Funciones de cadena SQL
- Funciones de cadena T-SQL
- Funciones de cadena de PostgreSQL