
Ejemplo de fórmula de desviación estándar (tabla de contenido)
- Fórmula
- Ejemplos
Muestra de fórmula de desviación estándar
En estadística, la desviación estándar es básicamente una medida para encontrar la dispersión de los valores del conjunto de datos del valor medio del conjunto de datos. Mide la distancia de ese punto de datos y la media. Entonces, cuanto mayor sea la desviación estándar, mayor será la dispersión y los puntos de datos tenderán a estar lejos de la media. Del mismo modo, una desviación estándar más baja significa que los puntos de datos estarán más cerca de la media. Es muy útil para comparar conjuntos de datos que pueden tener el mismo valor medio pero un rango diferente.
Por lo general, calcule la desviación estándar de los datos de la población, pero a veces los datos de la población son tan grandes que no es posible encontrar la desviación estándar para eso. En ese caso, se calcula la desviación estándar de la muestra y se convertirá en el representante de la desviación estándar de la población. Asumiremos que la muestra es la representación correcta de la población y nos centraremos en la desviación estándar de la muestra en este artículo.
Supongamos que tiene un conjunto de datos X con puntos de datos (X1, X2 …… ..Xn).
La fórmula para la desviación estándar de la población viene dada por:
Population Standard Deviation = √ (Σ (X i – X m ) 2 / n )
En caso de que no reciba toda la población y solo tenga una muestra (Digamos que X es el conjunto de datos de muestra de la población), entonces la fórmula para la desviación estándar de la muestra viene dada por:
Sample Standard Deviation = √ (Σ (X i – X m ) 2 / (n – 1))
Dónde:
- X i - i th valor del conjunto de datos
- X m : valor medio del conjunto de datos
- n - Número total de puntos de datos
La fórmula puede parecer confusa al principio, pero realmente es para trabajar. Los siguientes son los pasos que se pueden seguir para calcular la desviación estándar de la muestra:
- Encuentre el número de puntos en el conjunto de datos, es decir, n
- Luego, el siguiente paso es encontrar el valor medio de la muestra. Básicamente es el promedio de todos los valores.
- Después de eso, para cada punto de datos, encuentre la diferencia de eso de la media y luego al cuadrado.
- Tome la suma de todos los valores en el paso anterior y divídalo por n-1.
- El último paso es sacar la raíz cuadrada del número calculado anteriormente.
Hay otra forma de calcular la población y la desviación estándar simplemente usando la función STDEV.P () para la desviación estándar de la población y la función STDEV.S () para la desviación estándar de la muestra en Excel.
Ejemplos de fórmula de desviación estándar de muestra (con plantilla de Excel)
Tomemos un ejemplo para comprender el cálculo de la desviación estándar de muestra de una mejor manera.
Puede descargar esta plantilla de Excel de fórmula de desviación estándar de muestra aquí - Plantilla de Excel de fórmula de desviación estándar de muestraEjemplo de fórmula de desviación estándar - Ejemplo # 1
Digamos que tenemos dos conjuntos de datos de muestra A y B y cada uno contiene 20 puntos de datos aleatorios y tienen la misma media. Calcule la desviación estándar de muestra para el conjunto de datos A y B.
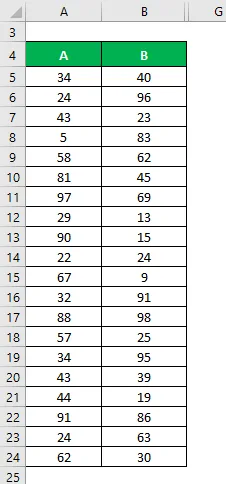
Solución:
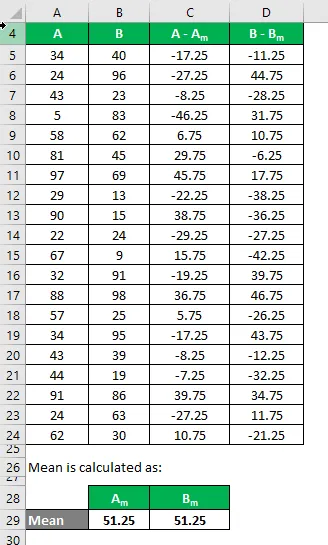
La media se calcula como:
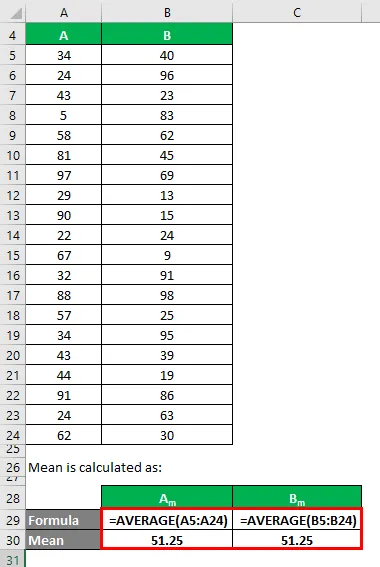
- Media del conjunto de datos A = 51.25
- Media del conjunto de datos B = 51.25
Ahora, necesitamos calcular la diferencia entre los puntos de datos y el valor medio.
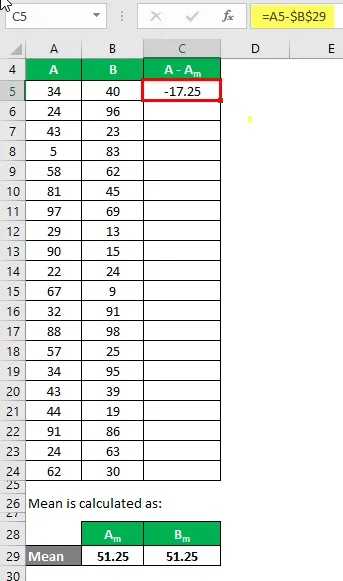
Del mismo modo, calcule para todo el conjunto de datos de A.
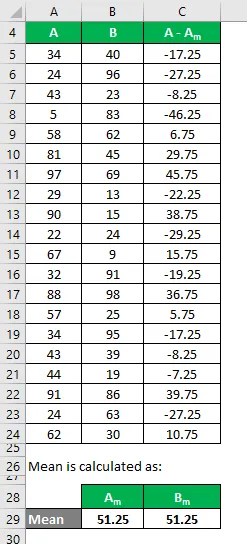
Del mismo modo, calcule también para el conjunto de datos B.
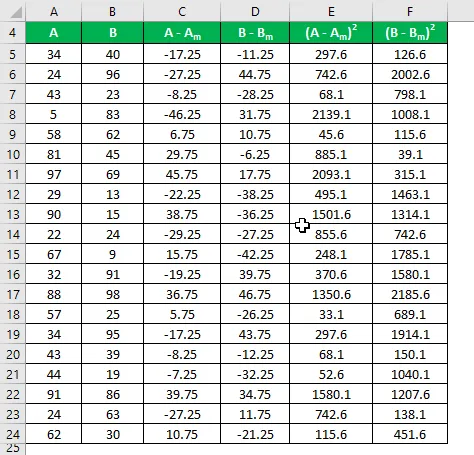
Calcule el cuadrado de la diferencia para los conjuntos de datos A y B.
La desviación estándar de muestra se calcula utilizando la fórmula que se proporciona a continuación
Desviación estándar de muestra = √ (Σ (X i - X m ) 2 / (n - 1))
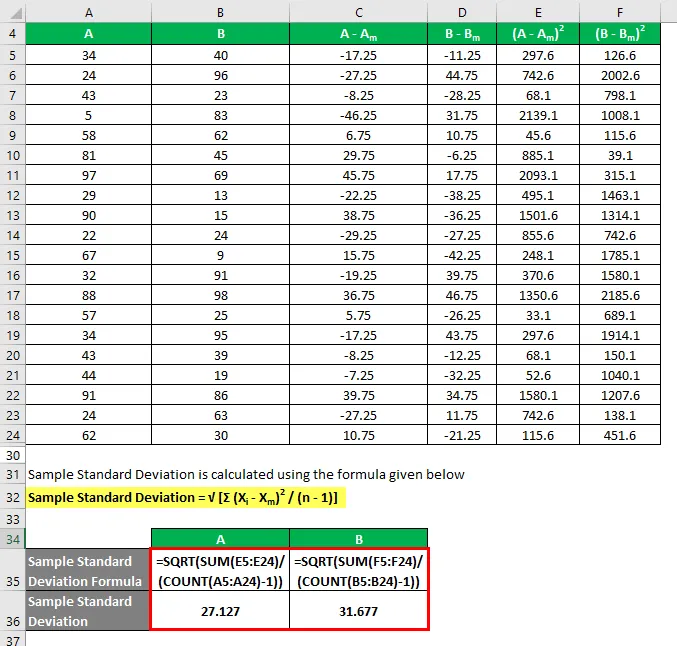
Entonces, si ve aquí, aunque ambos conjuntos de datos tienen el mismo valor medio, B tiene una desviación más estándar que A, lo que significa que los puntos de datos de B están más dispersos que A.
Ejemplo de fórmula de desviación estándar - Ejemplo # 2
Digamos que usted es un inversor muy reacio al riesgo y que busca invertir dinero en el mercado de valores. Dado que su apetito por el riesgo es bajo, desea invertir en acciones seguras que tengan una desviación estándar más baja. Su asesor financiero le ha sugerido 4 acciones entre las que puede elegir. Desea seleccionar 2 acciones entre esas 4 y lo decidirá sobre la base de una desviación estándar más baja.
Tienes información sobre sus rendimientos históricos de los últimos 15 años.
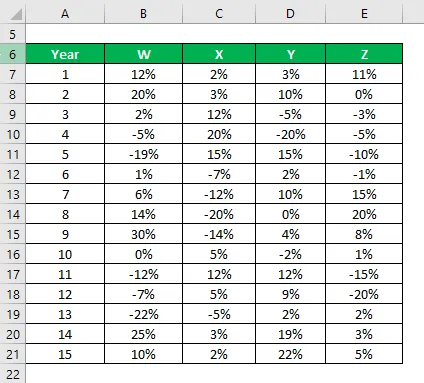
Solución:
La desviación estándar de muestra se calcula utilizando la fórmula de Excel
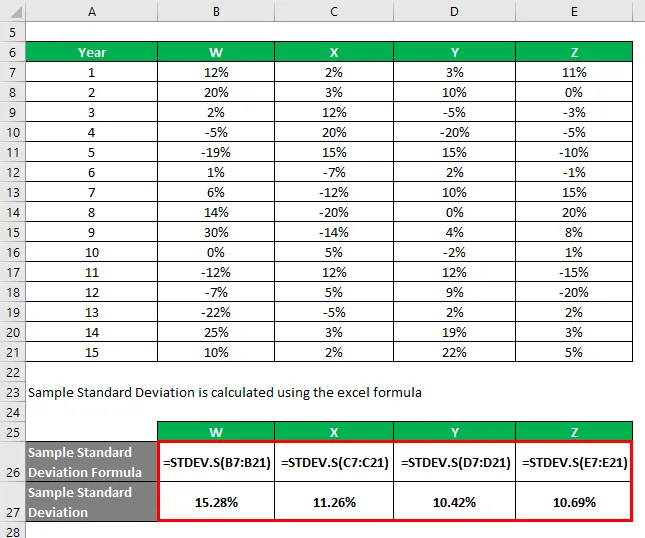
Según la información y la desviación estándar de muestra, elegirá las acciones Y y Z para invertir, ya que tienen la desviación estándar más baja.
Explicación
Discutimos el significado de la desviación estándar desde un punto de vista estadístico, pero también juega un papel vital si hablamos de un punto de vista financiero. En finanzas, es básicamente la medida del riesgo que conlleva una inversión y cuán riesgosa es esa inversión. Según el riesgo que tiene una inversión, los inversores pueden calcular el rendimiento mínimo que requieren para compensar ese riesgo. Como en el ejemplo anterior, dado que Y y Z tienen una desviación estándar menor, significa que hay una menor variabilidad en el rendimiento de estas existencias, por lo que son menos riesgosas. Un punto al usar la herramienta de desviación estándar debemos tener en cuenta que está muy afectado por los valores extremos o valores atípicos. Estos valores atípicos pueden sesgar el valor de la desviación estándar.
Relevancia y usos de la fórmula de muestra de desviación estándar
La desviación estándar ayuda a los inversores y al analista a encontrar el índice de riesgo y recompensa o el índice de Sharpe para una inversión. Básicamente, cualquiera puede obtener una tasa de rendimiento sin riesgo invirtiendo en valores del Tesoro y sin riesgo. Pero el rendimiento más allá de esto es el exceso de rendimiento y para lograrlo, cuál es el nivel de riesgo que uno necesita tomar es una medida de la relación de Sharpe:
Ratio de Sharpe = (Retorno de la inversión - Tasa libre de riesgo) / Desviación estándar
Para aumentar la relación de Sharpe, mejor es la inversión.
Como dijimos, la desviación estándar es una medida de riesgo, pero no siempre se prefiere un valor de desviación estándar más bajo. Si un inversor tiene un mayor apetito por el riesgo y quiere invertir de manera más agresiva, estará dispuesto a asumir más riesgos y preferirá una desviación estándar relativamente más alta que un inversor que no quiera el riesgo. Por lo tanto, todo depende del nivel de riesgo que un inversionista esté dispuesto a asumir.
Artículos recomendados
Esta ha sido una guía para la Fórmula de desviación estándar de muestra. Aquí discutimos cómo calcular la desviación estándar de muestra junto con ejemplos prácticos y una plantilla de Excel descargable. También puede consultar los siguientes artículos para obtener más información:
- Ejemplos de fórmula de varianza poblacional
- Calculadora para desviación estándar relativa
- ¿Cómo calcular la distribución normal estándar?
- Cálculo de distribución binomial